TrivialDB - 一个简单的SQL引擎

TrivialDB是一个简单的数据库管理系统，我们实现了大部分常见的SQL语句和类型。同时支持多表连接、复杂表达式运算、多主键约束、外键约束、CHECK约束、UNIQUE和DEFAULT约束、聚集查询、利用B+树索引的查询优化，同时，我们支持任意长度的VARCHAR类型。

FPGA Console - 硬件实现的 VT220 兼容终端

这是和HarryChen在这学期数字逻辑课上做的项目。主要是利用FPGA模拟一个终端。项目放在https://github.com/miskcoo/fpga-virtual-console上。

程序设计训练 - 数独、国际跳棋、人物信息检索系统

这次程序设计训练小学期一共有三个大作业，分别是数独、在线国际跳棋和人物信息检索系统。这里是简单的一些介绍，代码放在 https://github.com/miskcoo/programming-training。

Vim 里一些好用的插件

我主要是想要把一些用过的好用的插件记下来，万一哪天换了系统还可以在这里找回来。

较短步数复原魔方的算法

这其实是我们上学期程序设计课的一个大作业，我很早就想把它记录下来了，可是实在太懒了就拖到了这个学期。本来作业是要求复原魔方就好了，但是后来发现没有图形界面的话似乎调试很困难，就顺便写了一个 UI，刚好还学了一下 OpenGL。最开始我是写了能够找到最优解的 Krof 算法，但是估计是我写得比较丑再加上状态空间实在太大了（大约在搜索到第 15 步还是 16 步的时候状态数就到百亿级别了，而我 8 个线程一秒只能搜几千万个状态好像），根本没有办法在可以接受的时间内得到解。于是退而求其次，改为去搜索一个比较优的解，最后基本上一秒以内就可以得到解了。

上帝的指纹 — Mandelbrot 集合的绘制

曼德博集合（Mandelbrot Set）是一个在复平面上的点集。有人认为 Mandelbrot 集合是“人类有史以来做出的最奇异、最瑰丽的几何图形”，曾被称为“上帝的指纹”。

CodeChef 上一道有趣的网络流题目

这是一道2016年二月CodeChef上的一道题目，叫做Call Center Schedule。

题目大意是这样的：

一个电话公司有 $P$ 个员工，一个星期有 $D$ 天，每天需要工作 $H$ 个小时。每个员工在每个小时只能做参加会议和与客户通话两件事情中的一件，或者不做。

现在要为安排一个和客户通话的时间表，要求满足

• 每个人每天最多花费 $N$ 个小时在参加会议和通话上
• 第 $i$ 个人每周最多花费 $L_i$ 个小时和客户通话
• 每个人每天在 $LT_\text{begin}$ 到 $LT_\text{end}$ 的时间内至少要有 $1$ 小时没有被安排任务
• 对于第 $i$ 天第 $j$ 个小时，恰好有 $R_{i, j}$ 个人可以和客户通话

另外，开会的时间表已经安排完成，如果 $F_{k, i, j}$ 是 $0$ 则表示第 $k$ 个人在第 $i$ 天的第 $j$ 个小时开会，如果是 $1$ 则表示他可以被安排去和客户通话。

时限是 2s，最多 5 组数据，并且 $1 \leq N \leq H \leq 70$, $1 \leq D, P \leq 70$, $1 \leq L_i \leq ND$, $0 \leq R_{i, j} \leq 15$, $F_{k, i, j} \in {0, 1}$, $1 \leq LT_{begin} \leq LT_{end} \leq N$。

Tarjan 算法寻找有向图的强连通分量

在图论中，一个有向图被成为是强连通的（strongly connected）当且仅当每一对不相同结点 u 和 v 间既存在从 u 到 v 的路径也存在从 v 到 u 的路径。有向图的极大强连通子图（这里指点数极大）被称为强连通分量（strongly connected component）。

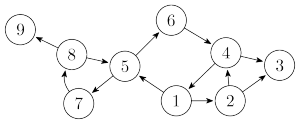
比如说这个有向图中，点 $1, 2, 4, 5, 6, 7, 8$ 和相应边组成的子图就是一个强连通分量，另外点 $3, 9$ 单独构成强连通分量。

Tarjan 算法是由 Robert Tarjan 提出的用于寻找有向图的强连通分量的算法。它可以在$\mathcal O(|V|+|E|)$的时间内得出结果。

Tarjan 算法主要是利用 DFS 来寻找强连通分量的。在介绍该算法之前，我们先来介绍一下搜索树。先前那个有向图的搜索树是这样的：

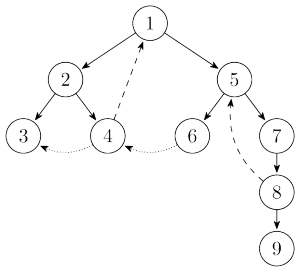
有向图的搜索树主要有 4 种边（这张图只有 3 种），其中用实线画出来的是树边（tree edge），每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。用长虚线画出来的是反祖边（back edge），也被叫做回边。用短虚线画出来的是横叉边（cross edge），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前节点的祖先时形成的。除此之外，像从结点1到结点6这样的边叫做前向边（forward edge），它是在搜索的时候遇到子树中的结点的时候形成的。

反演魔术：反演原理及二项式反演

首先我来说说什么是反演（inversion），对于一个数列$\{f_n\}$来说，如果我们知道另外一个数列$\{g_n\}$，满足如下条件 \[ g_n = \sum_{i=0}^n a_{ni}f_i \] 反演过程就是利用 $g_0, g_1, \cdots, g_n$ 来表示出 $f_n$ \[ f_n = \sum_{i = 0}^n b_{ni}g_i \] 本质上来说，反演其实是一个解线性方程组的过程，但是你观察后发现，这个矩阵实际上是一个三角矩阵，那必然存在着快捷的方法。对于使得这两个反演公式成立的这些系数应该满足什么条件呢？我们现在就来探讨一番！ 我们首先讨论一下在什么情况下能够比较容易建立反演公式，之后介绍二项式反演以及它的两个应用，其中一个是错位排列问题

Catalan 数列及其应用

卡特兰数（Catalan number）是组合数学中一个重要的计数数列，在很多看似毫不相关地方都能见到它的身影

这篇文章介绍卡特兰数的几个应用以及它的推导过程，从组合推理和生成函数两个方面来推导出 Catalan 数的公式

带限制条件的路径总数

首先我们来看一个问题：

在一个平面直角坐标系中，只能往右或往上走一个单位长度，问有多少种不同的路径可以从左下角 $(1, 1)$ 走到右上角 $(n, n)$，并且要求路径不能经过直线 $y = x$ 上方的点，下图中的路径都是合法的（图片来源 Wikipedia）

如果没有限制条件，那么从左下角走到右上角一共有 $2n$ 步，有 $n$ 步是往右，另外 $n$ 步是往上，那么路径方案数就是 $2n$ 步中选择 $n$ 步往右，一共有 ${2n} \choose {n}$ （即 $C_{2n}^n$）种方案

那么我们考虑一下这里面有多少种方案是不合法的

首先对于每一种不合法的方案，它的路径一定与 $y = x + 1$ 有交。我们找到它与 $y = x + 1$ 的第一个交点，然后将这个点后面部分的路径关于 $y = x + 1$ 做一个对称。由于原来路径到达 $(n, n)$，新的对称之后的路径就会到达 $(n - 1, n + 1)$。这样我们把每一种不合法方案都对应到了一条从 $(1, 1)$ 到 $(n - 1, n + 1)$ 的路径，现在再来看是否每一条这样的路径都能对应到一种不合法方案，如果是，那么这就建立了一个一一映射的关系，也就是它们的方案总数相同。这是肯定的，因为每一条这样的路径必定与 $y = x + 1$ 有交，那么对称回去，就得到一条不合法方案

由于从 $(1, 1)$ 到 $(n - 1, n + 1)$ 的路径有 ${n - 1 + n + 1} \choose {n - 1}$ 条，那么合法的方案就是

\[C_n = { {2n} \choose {n} } - { {2n} \choose {n - 1} } = \frac{1}{n + 1} { {2n} \choose {n} }\]

我们把这个方案数记为 $C_n$，这就是著名的 Catalan 数