-
BZOJ-3695. 滑行
这是 2014 年福建省省队训练的时候首长出的一道题，题目大概是这样的
首长NOI惨跪，于是去念文化课了。现在，他面对一道物理题
现在有一个小滑块可以在地面上滑行，地面上被划分成不同的区域，使得小滑块在不同的区域内部有一个不同的速度上限
小滑块在 $(0，0)$ 点，我们现在要推动小滑块到目标点 $(x, y)$
地面上有 $N$ 层区域，每层区域都是矩形，现在给你一个序列 ${H_i}$ 表示每层区域的高度，覆盖的地面横坐标范围是 $0\sim X$，第 $i$ 个区域的限速是 $v_i$
注： $Y=\sum_{i=1}^nH_i$，其它的地方小滑块不允许进入
现在我们要设计一个路线使得小滑块滑到目标点的用时最小
-
NOI2012. 迷失游乐园
放假了，小Z觉得呆在家里特别无聊，于是决定一个人去游乐园玩
进入游乐园后，小Z看了看游乐园的地图，发现可以将游乐园抽象成有 $n$ 个景点、$m$ 条道路的无向连通图，且该图中至多有一个环（即 $m$ 只可能等于 $n$ 或者 $n-1$，并且环上节点个数不超过 $25$ 个）。小Z现在所在的大门也正好是一个景点
小Z不知道什么好玩，于是他决定，从当前位置出发，每次随机去一个和当前景点有道路相连的景点，并且同一个景点不去两次（包括起始景点）。贪玩的小Z会一直游玩，直到当前景点的相邻景点都已经访问过为止。小Z所有经过的景点按顺序构成一条非重复路径，他想知道这条路径的期望长度是多少？
小Z把游乐园的抽象地图画下来带回了家，可是忘了标哪个点是大门，他只好假设每个景点都可能是大门（即每个景点作为起始点的概率是一样的）
同时，他每次在选择下一个景点时会等概率地随机选择一个还没去过的相邻景点
这题是 NOI2012 的一道题目，前几天突然想找一题环套树的来做一做于是就找到了这题
-
Karatsuba 乘法
Karatsuba 乘法是一种快速的乘法算法，它是由 Anatolii Alexeevitch Karatsuba 在 1960 年发现，并且在 1962 年公开发表的算法。 传统的高精度乘法复杂度会达到 $n^2$，而 Karatsuba 乘法则是基于分治策略，复杂度是 $3n^{\log_23}$，近似值大约为 $3n^{1.585}$。
-
制作网页版幻灯片——impress.js
impress.js 是一个基于 CSS3 运行在现代浏览器上的表现框架，它的灵感来源于 prezi.com。如果你有一点 web 的基础，你可以用它来制作幻灯片，而且效果十分绚丽，你可以轻松地做出旋转、划动、缩放等特效。因为它是遵循 MIT 和 GPLv2+ 协议的，所以你可以对 impress.js 的源码做任意修改。而且，还有在线的所见即所得的编辑网站 Dyapos 以及 Strut 等
这里有 impress.js 的示例，打开后你将会看到这样的画面
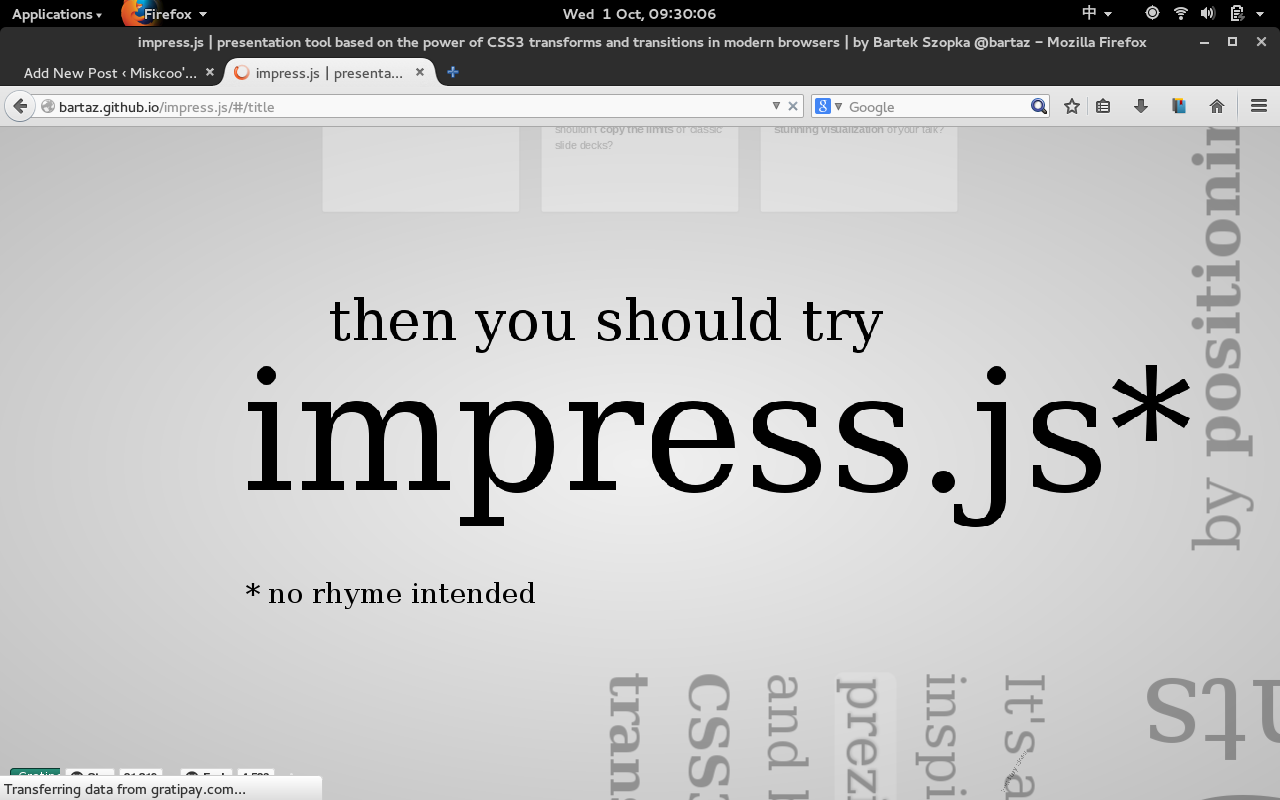
等不及了？那么，我们现在就来制作一个 impress.js 幻灯片
-
扩展欧几里得算法与中国剩余定理
在《孙子算经》中有这样一个问题：有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何?
这个问题说的是，有一件物品，我们不知道它的数量。但是，如果三个三个数，最后会剩下两个；如果五个五个数，最后会剩下三个；如果七个七个数，最后会剩下两个。问这个东西的数量是多少？
实际上，这个问题在现在我们可以将其转化为一个同余方程组：
[\left { \begin{aligned} x \equiv 2 \pmod 3 \ x \equiv 3 \pmod 5 \ x \equiv 2 \pmod 7 \end{aligned} \right.]
中国剩余定理告诉了我们像这样的同余方程组的解。这个定理又称为孙子定理，通常被简写成CRT（Chinese Remainder Theorem）。
这篇文章将会从欧几里得算法开始讲起，之后过渡到扩展欧几里得算法解线性方程，最后介绍中国剩余定理。
-
幂和
我们会介绍计算 $k$ 次幂和的递推公式。
-
「数论」线性求所有逆元的方法
前几天在看 lucas 定理的时候发现要求 $1,~2,\cdots,p-1\bmod p$ 的逆元，然后就看到了一个 $\Theta(n)$ 的做法。
-
FFT用到的各种素数
这几天在写 FFT，由于是在模意义下的，需要各种素数，然后就打了个表方便以后查。 如果 $r \cdot 2^k + 1$ 是个素数，那么在$\bmod r \cdot 2^k + 1$意义下，可以处理 $2^k$ 以内规模的数据，
-
BZOJ-3157. 国王奇遇记
题目大意是要求下面这个式子
\(\sum_{i=1}^n m^i \cdot i^m\)这个题目有三个版本：
这篇文章介绍 $\mathcal O(m^2)$ 和 $\mathcal O(m)$ 两种做法。