幂和

我们会介绍计算 $k$ 次幂和的递推公式。

首先我们从求前 $n$ 个整数的平方和开始，也就是

\[S_n = \sum_{i=1}^n n^2\]

然后可以尝试对 $S_n$ 进行“扰动”，就像这样

\[\begin{eqnarray*} S_n + (n + 1)^2 &=& \sum_{i=0}^n (i+1)^2 \\ &=& \sum_{i=0}^n (i^2 + 2i + 1) \\ &=& S_n + 2\sum_{i=1}^n i + (n + 1) \end{eqnarray*}\]

最后发现 $S_n$ 竟然被消掉了，“扰动”失败了，但是我们注意到这求出了 $\sum_{i=1}^n i$ 的公式。 我们可以考虑可不可以用更高的 $C_n = \sum_{i=1}^n i^3$ 来求出 $S_n$

\[\begin{eqnarray*}C_n + (n + 1)^3 &=& \sum_{i=0}^n (i+1)^3 \\ &=& \sum_{i=0}^n (i^3 + 3i^2 + 3i + 1) \\ &=& C_n + 3S_n + \frac{3n(n + 1)}{2} + (n + 1) \\ \Rightarrow S_n &=& \frac{(n+1)^3 - \frac{3n(n + 1)}{2} - (n + 1)}{3} \\ &=& \frac{n(n+\frac{1}{2})(n+1)}{3} \end{eqnarray*}\]

这样成功地求出了 $S_n$ 的公式，既然如此，我们又会去尝试计算更高阶的幂和。 首先，设

\[\begin{equation} \label{pow-sum} f_k(n) = \sum_{i=1}^n i^k \end{equation}\]

那么，我们会有

\[\begin{eqnarray*}f_{k+1}(n) + (n + 1)^{k+1} &=& 1 + \sum_{i=1}^n (i+1)^{k+1} \\ &=& 1 + \sum_{i=1}^n \sum_{j=0}^{k+1} { {k+1} \choose j} i^j \\ &=& 1 + \sum_{j=0}^{k+1} { {k+1} \choose j} \sum_{i=1}^n i^j \\ &=& 1 + \sum_{i=0}^{k+1} { {k+1} \choose i} f_i(n) \\ &=& 1 + f_{k+1}(n) + (k + 1) f_k(n) + \sum_{i=0}^{k - 1} { {k+1} \choose i} f_i(n) \ \end{eqnarray*}\]

这样就得到了

\[\begin{equation} \label{simplified-pow-sum} f_k(n) = \frac{(n+1)^{k+1} - 1}{k + 1} - \frac{1}{k+1}\sum_{i=0}^{k - 1} { {k+1} \choose i} f_i(n) \end{equation}\]

或者我们可以写成

\[\begin{equation} f_{k-1}(n) = \frac{(n+1)^k - 1}{k} - \frac{1}{k}\sum_{i=0}^{k - 2} { {k} \choose i} f_i(n) \end{equation}\]

这个公式有什么意义呢？在计算机里，有了它我们就可以用 $\Theta(m^2)$ 的时间来计算 $f_m(n)$，这比原来暴力来说至少是一个进步

现在我们换一种方式来试试推导这个和式

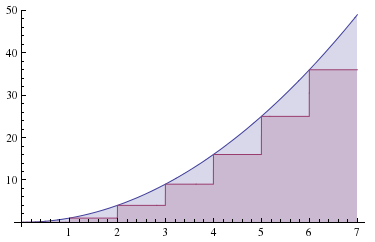
显然，我们要求的就是图中紫色部分的面积，因为有微积分这个工具，我们现在可以很容易地求出蓝色部分以及紫色部分面积的和，也就是

\[\int_1^{n+1} x^2 dx = \left .\frac{x^3}{3}\right | _1^{n+1} = \frac{(n+1)^3}{3} - \frac{1}{3}\]

我们可以考虑把误差扣掉，类似这样

\[\begin{eqnarray*} S_n &=& \int_1^{n+1} x^2 dx - \sum_{i=1}^n \left( \int_i^{i+1} x^2 dx - i^2 \right) \\ &=& \frac{(n+1)^3}{3} - \frac{1}{3} - \sum_{i=1}^n \left( \frac{(i+1)^3-i^3}{3} - i^2 \right) \\ &=& \frac{(n+1)^3}{3} - \frac{1}{3} - \sum_{i=1}^n \frac{3i+1}{3} \\ &=& \frac{n(n+\frac{1}{2})(n+1)}{3} \end{eqnarray*}\]

类似的，我们也可以用这种方法来计算 $f_k(n)$ \(\begin{eqnarray*} f_k(n) &=& \int_1^{n+1} x^k dx - \sum_{i=1}^n \left( \int_i^{i+1} x^k dx - i^k \right) \\ &=& \frac{(n+1)^{k+1} - 1}{k+1} - \sum_{i=1}^n \frac{(i+1)^{k+1}-i^{k+1}-(k+1)i^k}{k+1} \\ &=& \frac{(n+1)^{k+1} - 1}{k+1} - \frac{1}{k+1} \sum_{i=1}^n \left((i+1)^{k+1}-i^{k+1}-(k+1)i^k\right) \\ &=& \frac{(n+1)^{k+1} - 1}{k+1} - \frac{1}{k+1} \sum_{i=1}^n \sum_{j=0}^{k-1} { {k+1} \choose j} i^j \\ &=& \frac{(n+1)^{k+1} - 1}{k+1} - \frac{1}{k+1} \sum_{i=0}^{k-1} { {k+1} \choose i} f_i(n) \end{eqnarray*}\)