• Jun 18, 2015

    Codeforces 上的一些组合计数问题

    Codeforces 15E. Triangles

    Problem：给出一个有规律的金字塔（如图），黑色的边是可以走路径，要求求出包含 $H$ 点的简单回路（不经过一个顶点两次）的条数，并且这个回路围住的部分不可以包含灰色的三角形，答案对 $10^9+9$ 取模，其中 $n \leq 10^6$，并且一定是一个偶数

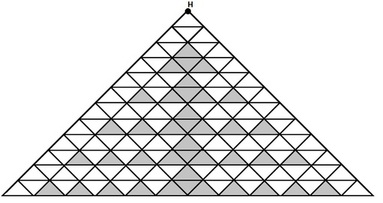
    Example：当 $n = 2$ 时，一共有 $10$ 种方案，其中 $5$ 种是这样，另外的是顺时针顺序地走

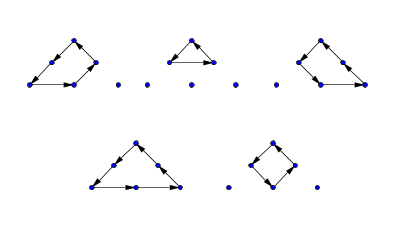
    Solution：首先第 $1$ 层是最特殊的，因为这里没有灰色的三角形，然后注意到灰色的部分把整个金字塔分成了左部和右部

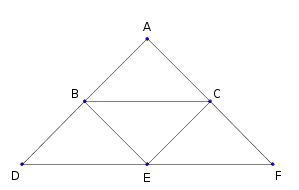
    路径现在可以分成三个部分

    • 在第一层移动，这一共 $10$ 种（见样例）
    • 进入左部或右部后直接回到 $H$
    • 进入左部（右部）后经过 $E$ 点进入右部（左部）

    对于第二种情况，在第一层的部分走法可以是（只有逆时针部分，实际上有 $8$ 种）

    • $A \rightarrow B \rightarrow D \rightarrow \text{LeftPart} \rightarrow E \rightarrow C \rightarrow A$
    • $A \rightarrow B \rightarrow D \rightarrow \text{LeftPart} \rightarrow E \rightarrow F \rightarrow C \rightarrow A$
    • $A \rightarrow B \rightarrow E \rightarrow \text{RightPart} \rightarrow F \rightarrow C \rightarrow A$
    • $A \rightarrow B \rightarrow D \rightarrow E \rightarrow \text{RightPart} \rightarrow F \rightarrow C \rightarrow A$

    对于第三种情况，在第一层（原来图中的两层现在算一层，也就是下面的 $n$ 是题目中 $n$ 的 $\frac{1}{2}$）的部分走法有 $2$ 种，左部到右部和右部到左部

    现在要统计的就是在左部和右部内有多少种方案，因为左部右部对称，所以答案是一样的，我们来考虑左部

    用 $S_n$ 表示在有 $n$ 层的金字塔中，走左部的方案数，因为走进左部后每一层都会遇到凹进去的部分，这部分只要枚举一下走了多远可以统计出第 $n$ 层一共有 $2\sum_{i=1}^{n-2} 2^i + 1 = 2^n - 3$ 这么多的情况

    然后要走到第 $n$ 层后就是 $\prod_{i=2}^{n} (2^i - 3)$ 种情况，然后走回去的路径有 $4$ 种选择，因此

    \[ S_n = \sum_{i=2}^{n} 4\prod_{j=2}^i (2^j - 3) \]

    答案是 $2S_n^2 + 8S_n + 10$

  • Jun 8, 2015

    牛顿迭代法在多项式运算的应用

    总算是快把 FFT 和生成函数的各种东西补了好多，膜拜策爷的论文和 Picks 的博客！

    这篇文章大概就是说如何用牛顿迭代法来解满足 $G(F(z)) \equiv 0 \pmod {z^n}$ 的 $F(z)$

    然后这东西可以比较方便地计算 $\sqrt{A(z)}$、$e^{A(z)}$，也就是多项式开根、求指数对数之类鬼畜的东西，在生成函数计数中十分有用

    顺便一提，这里说的“多项式”实际上你可以直接理解为生成函数或者形式幂级数

  • May 29, 2015

    平面图转对偶图及点定位

    平面图（planar graph）就是一个可以在平面上画出来的图，并且所有的边只在顶点处相交。平面图的对偶图（dual graph）是将这个平面的每个区域看成点，原图每一条边所属的两个相邻的区域对应在对偶图中的点有连边

    比如下面这张图（来源于 Wikipedia）

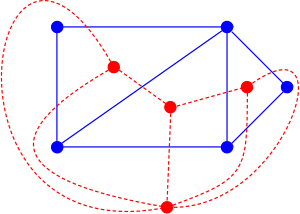
    蓝色的部分就是一个平面图，红色的就是它的对偶图

    平面图的点定位（point location）就是找出一个点属于这个图的哪个区域

    这篇文章介绍如何将一个平面图转换为其对偶图，和基于扫描线的离线的点定位算法

  • May 28, 2015

    BZOJ-3456. 城市规划

    题目要求求出有 $n (n \leq 130000)$ 个点的有标号简单连通无向图的个数，答案 $\bmod 1004535809$ $(479 \times 2^{21} + 1)$，是个质数

    比如三个点的情况

    题目链接：BZOJ-3456

  • May 25, 2015

    多项式的多点求值与快速插值

    多项式的多点求值（multi-point evaluation）是给出一个多项式 $A(x)$，和 $n$ 个点 $x_0, x_1, \cdots, x_{n-1}$，要求求出 $A(x_0), A(x_1), \cdots, A(x_{n-1})$

    相反的，多项式的插值（interpolation）是给出 $n+1$ 个点 $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$，求出一个 $n$ 次多项式，使得这些点都在这个多项式上

    这两个问题实际上是在多项式的点值表示（point-value representation）和系数表示（coefficient representation）之间转换的方法，在快速傅里叶变换中由于带入值的特殊性质，可以在 $\mathcal O(n\log n)$ 的之间内将两种东西互相转换，但是，如果是任意给定点要求求值或者插值，就没有比较好的性质可以利用，但是仍然有比较快速的方法来计算它们

  • May 23, 2015

    BZOJ-3435. [Wc2014]紫荆花之恋

    强强和萌萌是一对好朋友。有一天他们在外面闲逛，突然看到前方有一棵紫荆树。这已经是紫荆花飞舞的季节了，无数的花瓣以肉眼可见的速度从紫荆树上长了出来。

    仔细看看的话，这个大树实际上是一个带权树。每个时刻它会长出一个新的叶子节点，每个节点上有一个可爱的小精灵，新长出的节点上也会同时出现一个新的小精灵。小精灵是很萌但是也很脆弱的生物，每个小精灵 $i$ 都有一个感受能力值 $r_i$，小精灵 $i,j$ 成为朋友当且仅当在树上 $i$ 和 $j$ 的距离 $\text{dist}(i,j) \leq r_i+r_j$，其中 $\text{dist}(i,j)$ 表示在这个树上从 $i$ 到 $j$ 的唯一路径上所有边的边权和。

    强强和萌萌很好奇每次新长出一个叶子节点之后，这个树上总共有几对朋友。

    我们假定这个树一开始为空，节点按照加入的顺序从 $1$ 开始编号。由于强强非常好奇，你必须在他每次出现新结点后马上给出总共的朋友对数，不能拖延哦。

    【输入格式】

    第一行包含一个整数，表示测试点编号。

    第二行包含一个正整数 $n$，表示总共要加入的节点数。

    我们令加入节点前的总共朋友对数是 $\text{last_ans}$，在一开始时它的值为 $0$。

    接下来 $n$ 行中第 $i$ 行有三个非负整数 $ai,ci,ri$，表示结点 $i$ 的父节点的编号为 $a_i \oplus (\text{last_ans} \bmod 10^9)$（其中 $\oplus$ 表示异或，$\text{mod}$ 表示取余，数据保证这样操作后得到的结果介于 $1$ 到 $i-1$ 之间），与父结点之间的边权为 $c_i$，节点 $i$ 上小精灵的感受能力值为 $r_i$。

    注意 $a_1=c_1=0$，表示 $1$ 号节点是根结点，对于 $i>1$，父节点的编号至少为 $1$。

    【输出格式】

    包含 $n$ 行，每行输出 $1$ 个整数，表示加入第 $i$ 个点之后，树上有几对朋友。

    【数据范围】

    $n \leq 10^5$，$1 \leq c_i \leq 10^4$，$a_i \leq 2\times 10^9$，$r_i \leq 10^9$，时限 12s

  • May 22, 2015

    多项式求除法及求模

    问题是这样的：给定一个 $n$ 次多项式 $A(x)$ 和一个 $m(m \leq n)$ 次多项式 $B(x)$，要求求出两个多项式 $D(x), R(x)$，满足

    \[ \begin{equation} \label{div0} A(x) = D(x)B(x) + R(x) \end{equation} \]

    并且 $deg D \leq degA - degB = n - m$，$degR < m$

    在解决这个问题之前你需要掌握多项式求逆，利用快速傅里叶变换可以在 $\mathcal O(n\log n)$ 的复杂度内求出这个问题的解

    多项式除法在很多问题中都有应用，例如多项式的扩展欧几里得算法、线性递推的优化等等

  • May 21, 2015

    BZOJ-3557. [Ctsc2014]随机数

    露露、花花和萱萱最近对计算机中的随机数产生了兴趣。为大家所熟知的是，由计算机生成的随机数序列并非真正的随机数，而是由一定法则生成的伪随机数。

    某一天，露露了解了一种生成随机数的方法，称为 Mersenne twister。给定初始参数 $m \in \mathbb Z^+$，$x \in \mathbb Z \cap [0, 2^m)$ 和初值 $M_0 \in \mathbb Z \cap [0, 2^m)$，它通过下列递推式构造伪随机数列 ${M_n}$：

    [ \begin{equation} M_n = \left { \begin{aligned} &2M_{n-1}& ~2M_{n-1} < 2^m \ (2M_{n-1} &-2^m) \oplus x & ~2M_{n-1} \geq 2^m \ \end{aligned} \right. \end{equation} ]

    其中 $\oplus$ 是二进制异或运算（C/C++ 中的 ^ 运算）。而参数 $x$ 的选取若使得该数列在长度趋于无穷时，近似等概率地在 $\mathbb Z \cap (0, 2^m)$ 中取值，就称 $x$ 是好的。例如，在 $m > 1$ 时 $x=0$ 就显然不是好的。

    在露露向伙伴介绍了 Mersenne twister 之后，花花想用一些经典的随机性测试来检验它的随机性强度。为此，花花使用计算机计算了一些 $M_k$。

    但细心的萱萱注意到，花花在某次使用二进制输入 $k$ 时，在末尾多输入了 $l$ 个 $0$。她正想告诉花花这个疏忽，然而花花已经计算并记录了错误的 $M_k$ 值而没有记录 $k$ 的值。虽然这其实不是什么致命的问题，但是在萱萱告诉花花她的这个疏漏时，作为完美主义者的花花还是恳求萱萱帮她修正 $M_k$ 的值。萱萱便把这个任务交给了他的 AI ——你！

    【输入格式】

    输入文件 random.in 的第一行包含一个正整数 $m$，第二行为二进制表示的 $x$（共 $m$ 个数，从低位到高位排列），第三行为二进制表示的 $M_0$（排列方式同 $x$），第四行包含一个整数 $type$。

    接下来分为两种可能的情况：

    1. $type = 0$（萱萱记下了花花的输入）：则第五行包含一个整数，表示萱萱记下来的正确的 $k$ 值。
    2. $type = 1$（萱萱未能记下花花的输入）：则第五行为 $l$，第六行输入花花计算出错误的二进制表示的 $M_k$。

    【输出格式】

    输出文件 random.out 仅一行，为一个 $m$ 位的 01 串，表示你求得的正确的 $M_k$（同样要求从低位到高位排列）

    【数据范围】

    对于 $type = 0$ 的部分，$m, k \leq 10^6$

    对于 $type = 1$ 的部分，$m \leq 10^3, k \leq 10^{18}, l \leq 10$，$x$ 是“好的”

    每个数据点时限 20s，并且开启编译器优化

  • May 19, 2015

    扩展大步小步法解决离散对数问题

    离散对数（Discrete Logarithm）问题是这样一个问题，它是要求解模方程

  • May 16, 2015

    BZOJ-3812. 主旋律

    题目给出一个 $n$ 个点，$m$ 条边的有向图，要求求出删掉一些边以后，整个图强联通的方案数，其中 $n \leq 15, m \leq n(n-1)$

    样例是这样的，十分良心，一共有 $9390$ 种方案

    题目链接：BZOJ-3812