Codeforces 15E. Triangles

Problem：给出一个有规律的金字塔（如图），黑色的边是可以走路径，要求求出包含 $H$ 点的简单回路（不经过一个顶点两次）的条数，并且这个回路围住的部分不可以包含灰色的三角形，答案对 $10^9+9$ 取模，其中 $n \leq 10^6$，并且一定是一个偶数

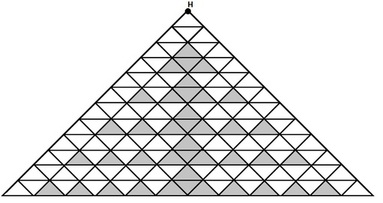
Example：当 $n = 2$ 时，一共有 $10$ 种方案，其中 $5$ 种是这样，另外的是顺时针顺序地走

Solution：首先第 $1$ 层是最特殊的，因为这里没有灰色的三角形，然后注意到灰色的部分把整个金字塔分成了左部和右部

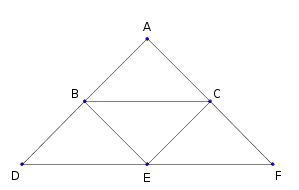
路径现在可以分成三个部分

  • 在第一层移动，这一共 $10$ 种（见样例）
  • 进入左部或右部后直接回到 $H$
  • 进入左部（右部）后经过 $E$ 点进入右部（左部）

对于第二种情况，在第一层的部分走法可以是（只有逆时针部分，实际上有 $8$ 种）

  • $A \rightarrow B \rightarrow D \rightarrow \text{LeftPart} \rightarrow E \rightarrow C \rightarrow A$
  • $A \rightarrow B \rightarrow D \rightarrow \text{LeftPart} \rightarrow E \rightarrow F \rightarrow C \rightarrow A$
  • $A \rightarrow B \rightarrow E \rightarrow \text{RightPart} \rightarrow F \rightarrow C \rightarrow A$
  • $A \rightarrow B \rightarrow D \rightarrow E \rightarrow \text{RightPart} \rightarrow F \rightarrow C \rightarrow A$

对于第三种情况，在第一层（原来图中的两层现在算一层，也就是下面的 $n$ 是题目中 $n$ 的 $\frac{1}{2}$）的部分走法有 $2$ 种，左部到右部和右部到左部

现在要统计的就是在左部和右部内有多少种方案，因为左部右部对称，所以答案是一样的，我们来考虑左部

用 $S_n$ 表示在有 $n$ 层的金字塔中，走左部的方案数，因为走进左部后每一层都会遇到凹进去的部分，这部分只要枚举一下走了多远可以统计出第 $n$ 层一共有 $2\sum_{i=1}^{n-2} 2^i + 1 = 2^n - 3$ 这么多的情况

然后要走到第 $n$ 层后就是 $\prod_{i=2}^{n} (2^i - 3)$ 种情况，然后走回去的路径有 $4$ 种选择，因此

\[ S_n = \sum_{i=2}^{n} 4\prod_{j=2}^i (2^j - 3) \]

答案是 $2S_n^2 + 8S_n + 10$ 

#include <cstdio>

const long long mod_v = 1000000009;

int main()
{
	int n;
	std::scanf("%d", &n);
	long long pw = 2, g = 4, s = 0;
	while(n -= 2)
	{
		pw = (pw << 1) % mod_v;
		g = g * (pw - 3) % mod_v;
		s = (s + g) % mod_v;
	}

	int ans = (2 * s * s + 8 * s + 10) % mod_v;
	if(ans < 0) ans += mod_v;
	std::printf("%d\n", ans);
	return 0;
}

Codeforces 382E. Ksenia and Combinatorics

Problem：有一棵 $n(n \leq 50)$ 个节点的树，节点标号为 $1, 2, \cdots, n$，除了 $1$ 号节点最多会与其它 $2$ 个节点连边外，其余节点最多会与其它 $3$ 个节点连边，两棵树是相同的，当且仅当每个节点的相邻节点都相同，问有多少种不同的这样的树，满足它的最大匹配是 $k$，答案对 $10^9 + 7$ 取模

Solution：我们可以用 $f(n, k, {0, 1})$ 来表示有 $n$ 个节点的树，它的最大匹配是 $k$ 并且根节点是否在匹配中的方案数

现在和普通的二叉树计数一样，考虑枚举左右子树大小和最大匹配数，由于这树的节点是有标号的，假设左子树大小是 $n_1$，那么就有 ${n - 1} \choose n_1$ 种方案分配节点，然后还有 $n_1(n - n_1 - 1)$ 种方案分配根结点

为了避免重复统计，我们可以限制左子树的大小不超过右子树，特别的，当左右子树大小相同的时候，强制限定最小的那个节点在左子树，这样就可以避免重复了

假设根结点在匹配中，那么一定要有一个子树的根节点不在匹配中，这样才可以匹配

假设根节点不在匹配中，那么左右子树的根结点一定都要匹配，否则就不是最大匹配，因此只能从这里转移

#include <iostream>

typedef long long calc_t;
const int MaxN = 52, mod_v = 1000000007;
calc_t f[MaxN][MaxN >> 1][2], C[MaxN][MaxN];

void init_comb(int n)
{
	for(int i = 0; i <= n; ++i)
	{
		C[i][i] = C[i][0] = 1;
		for(int j = 1; j < i; ++j)
		{
			C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
			if(C[i][j] >= mod_v) C[i][j] -= mod_v;
		}
	}
}

int main()
{
	int n0, k0;
	std::cin >> n0 >> k0;
	if(k0 << 1 > n0)
	{
		std::cout << "0\n";
		return 0;
	}

	init_comb(n0);
	f[1][0][0] = 1; f[0][0][1] = 1;
	for(int n = 2; n <= n0; ++n)
	{
		for(int k = 1; k <= n >> 1; ++k)
		{
			for(int g = 0; g <= 1; ++g)
			{
				calc_t& val = f[n][k][g];
				for(int n1 = 0, n2 = n - 1; n1 <= n2; ++n1, --n2)
				{
					calc_t ways;
					if(n1 != n2) ways = C[n - 1][n1];
					else ways = C[n - 2][n1 - 1];
					if(n1) ways = ways * n1 * n2 % mod_v;
					else ways = ways * n2 % mod_v;

					for(int k1 = 0; k1 + g <= k; ++k1)
					{
						int k2 = k - k1 - g;
						if(g == 0) 
						{
							val += f[n1][k1][1] * f[n2][k2][1] % mod_v * ways % mod_v;
						} else {
							val += (f[n1][k1][1] * f[n2][k2][0]
								 + f[n1][k1][0] * f[n2][k2][1]
								 + f[n1][k1][0] * f[n2][k2][0]) % mod_v * ways % mod_v;
						}
					}

					val %= mod_v;
				}
			}
		}
	}

	std::cout << (f[n0][k0][0] + f[n0][k0][1]) % mod_v << std::endl;
	return 0;
}

Codeforces 28C. Bath Queue

Problem：有 $n$ 个人等概率随机进入 $m$ 个房间，一个房间可以有多个人，第 $i$ 个房间有 $a_i$ 个水龙头，在一个房间的人要去排队装水，他们会使得最长的队尽可能小，求所有房间中最长队列长度的期望

其中 $1 \leq n, m \leq 50, 1 \leq a_1, a_2, \cdots, a_m \leq 50$

Solution：由于要求期望，我们可以先求出最长队列长度为 $l$ 的有多少种方案。用 $f(i, j, l)$ 表示已经分配了前 $i$ 个房间和 $j$ 个人，最长队列长度为 $l$ 的方案数

首先什么人都没有的情况 $f(i, 0, 0) = 1$

现在答案可以从两个地方统计，一是当前房间队列达到 $l$，前面的房间任意，二是前面有房间队列达到 $l$，但是当前没有达到，那么可以列出方程

\[\begin{eqnarray*} f(i, j, l) &=& \sum_{k = 0}^l { {n - j + p_i} \choose {p_i}} f(i - 1, j - p_i, k)\\&+& \sum_{k=0}^{\min p_i - 1} { {n - j + k} \choose k} f(i - 1, j - k, l) \end{eqnarray*}\]

这里 $p_i$ 是使得第 $i$ 个房间队列长度为 $l$ 的数的集合，也是要求枚举的

#include <cstdio>
#include <algorithm>

const int MaxN = 55;
double C[MaxN << 1][MaxN << 1];
double f[MaxN][MaxN][MaxN];

double pow(double x, int p)
{
	double v = 1.0;
	for(; p; p >>= 1, x *= x)
		if(p & 1) v *= x;
	return v;
}

void init_comb(int n, int m)
{
	for(int i = 0; i <= n + m; ++i)
	{
		C[i][0] = C[i][i] = 1;
		for(int j = 1; j < i; ++j)
			C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
	}
}

int main()
{
	int n, m;
	std::scanf("%d %d", &n, &m);
	init_comb(n, m);

	f[0][0][0] = 1;
	for(int i = 1; i <= m; ++i)
	{
		int basins;
		std::scanf("%d", &basins);
		f[i][0][0] = 1;

		for(int j = 1; j <= n; ++j)
		{
			for(int l = 0; l <= j; ++l)
			{
				int b = basins * l, a = basins * (l - 1) + 1;
				for(int k = 0; k <= l; ++k)
				{
					for(int p = std::max(a, 0); p <= b && p <= j; ++p)
						f[i][j][l] += f[i - 1][j - p][k] * C[n - j + p][p];
				}

				for(int p = 0; p < a && p <= j; ++p)
					f[i][j][l] += f[i - 1][j - p][l] * C[n - j + p][p];
			}
		}
	}

	double ans = 0;
	for(int i = 1; i <= n; ++i)
		ans += f[m][n][i] * i;
	std::printf("%.14lf\n", ans / pow(m, n));
	return 0;
}

Codeforces 9D. How many trees?

Problem：题目要求统计有多少棵二叉树满足有 $n$ 个节点，并且高度不小于 $h$，其中 $n, h \leq 35$

Solution：这题和上题有些相似之处，可以用 $f(n, h)$ 表示有 $n$ 个节点，高度恰好为 $h$ 的方案数，那么考虑左右子树哪一棵高度是 $h - 1$ 来转移

\[f(n, h) = \sum_{i = 0}^{n-1}\sum_{j = 0}^{h-1}f(i, h - 1)f(n - i - 1, j) + \sum_{i = 0}^{n-1}\sum_{j = 0}^{h-2}f(i, h - 1)f(n - i - 1, j)\]

最后的答案是

\[\text{ans} = \sum_{i \geq h} f(n, i)\]

这样的话复杂度是 $\mathcal O(n^4)$ 的，注意到里面的求和是一个前缀和，记 $s(n, h) = \sum_{i=0}^h f(n, i)$，那么式子就可以变成

\[f(n, h) = \sum_{i = 0}^{n-1}f(i, h - 1)s(n - i - 1, h - 1) + \sum_{i = 0}^{n-1}f(i, h - 1)s(n - i - 1, h - 2)\]

这样复杂度变成了 $\mathcal O(n^3)$，实际上，注意到求和是个卷积的形式，用快速傅里叶变换，可以优化为 $\mathcal O(n^2\log n)$

我这里只给出用了前缀和优化的代码

#include <cstdio>

const int MaxN = 40;
long long f[MaxN][MaxN], prefix[MaxN];

int main()
{
	int n, h;
	std::scanf("%d %d", &n, &h);
	f[0][0] = 1;
	for(int i = 1; i <= n; ++i) 
	{ 
		for(int j = 0; j <= n; ++j) 
		{
			for(int k = 0; k != j; ++k) 
			{
//				for(int p = 0; p < i - 1; ++p)
//					f[i][j] += 2 * f[i - 1][k] * f[p][j - k - 1];
				f[i][j] += 2 * f[i - 1][k] * prefix[j - k - 1];
				f[i][j] += f[i - 1][k] * f[i - 1][j - k - 1];
			}
		}

		for(int j = 0; j <= n; ++j)
			prefix[j] += f[i - 1][j];
	}

	long long ans = 0;
	for(int i = h; i <= n; ++i)
		ans += f[i][n];
	std::printf("%I64d\n", ans);
	return 0;
}

Codeforces 37D. Lesson Timetable

Problem：有编号为 $1, 2, \cdots, m$ 一共 $m$ 个教室和编号为 $1, 2, \cdots, n$ 一共 $n$ 组学生，每一组学生要上 $2$ 节课，要求第一节上课的教室编号不能大于第二节上课的教室编号

第 $i$ 个教室还需要满足

  • 第一节课必须恰好有 $X_i$ 组学生在这里上课
  • 同一时间不能有超过 $Y_i$ 组学生在该教室上课

答案对 $10^9 + 7$ 取模，数据保证 $1 \leq m, X_i, Y_i \leq 100$ 且 $X_i \leq Y_i$

Example：当 $n = 3, X = Y = (1, 1, 1)$ 时，一共有 $3! = 6$ 种，因为所有人都不能够移动教室

Solution：我们先考虑对于第一节课确定的一种方案有多少种第二节课的安排，因为有只能往后移动教室这个限定，这个问题就有了明显的阶段性，用 $f(i, j)$ 表示前 $i$ 间教室，已经有 $j$ 组第二节课已经确定完教室了的方案数，为了方便，记 $S_n = \sum_{i=1}^n X_i$，这样考虑 $f(i, j)$ 可以给谁贡献答案，枚举第 $i + 1$ 个教室有多少人第二节会在这里上，假设有 $k$ 个，那么

\[f(i + 1, j + k) \leftarrow { {S_{i + 1} - j} \choose k}f(i, j)\]

枚举的 $k$ 的范围是 $[0, \min ( Y_i, S_{i + 1} - j ) ]$

然后最后还要计算出有多少种不同的第一节课方案，这乘上一个多项式系数就好了

\[\text{ans} = {S_n \choose {X_1, X_2, \cdots, X_n}}f(n, S_n)\] 
#include <cstdio>
#include <algorithm>

typedef long long calc_t;
const int MaxN = 110, MaxS = 1010;
const int mod_v = 1000000007;
int sum[MaxN], C[MaxS][MaxS], f[MaxN][MaxS];

int inc(int x, int v) { x += v; if(x >= mod_v) x -= mod_v; return x; }
void inc0(int& x, int v) { x = inc(x, v); }

int main()
{
	int n;
	std::scanf("%d", &n);
	for(int i = 1; i <= n; ++i)
	{
		std::scanf("%d", sum + i);
		sum[i] += sum[i - 1];
	}

	for(int i = 0; i <= sum[n]; ++i)
	{
		C[i][0] = C[i][i] = 1;
		for(int j = 1; j < i; ++j)
			C[i][j] = inc(C[i - 1][j - 1], C[i - 1][j]);
	}

	f[0][0] = 1;
	for(int i = 0; i != n; ++i)
	{
		int y;
		std::scanf("%d", &y);
		for(int j = 0; j <= sum[i]; ++j)
		{
			int tot = sum[i + 1] - j;
			for(int k = 0; k <= std::min(tot, y); ++k)
				inc0(f[i + 1][j + k], (calc_t)f[i][j] * C[tot][k] % mod_v);
		}
	}

	int ans = f[n][sum[n]];
	for(int i = 1; i <= n; ++i)
		ans = (calc_t)ans * C[sum[n] - sum[i - 1]][sum[i] - sum[i - 1]] % mod_v;
	std::printf("%d\n", ans);
	return 0;
}

Codeforces 51E. Pentagon

Problem：给出一个有 $n (n \leq 700)$ 个点 $m$ 条边的无向图，统计有多少个五元环

Solution：可以考虑枚举一个五元环上的两个点，如果能够找到两条长度为 $2$ 和 $3$ 的不相交路径，那么就认为找到了一个五元环

因此可以先用 $A_{u, v}$ 表示 $u$ 到 $v$ 有多少条长度为 $1$ 的路径，用 $B_{u, v}$ 表示有多少条长度为 $2$ 的路径，用 $C_{u, v}$ 表示有多少条长度为 $3$ 的路径（这里把 $u \rightarrow a \rightarrow u \rightarrow v$ 这样的路径也算进去）

因为 $B$ 可以由 $A$ 和 $A$ 组合而成，$C$ 可以由 $A$ 和 $B$ 组合而成，因此用类似 Floyd 的方法，可以在 $\mathcal O(n^3)$ 算出它们

然后来考虑如何统计答案，枚举五元环上两个点 $u, v$ 直接计算 $\sum_u \sum_v B_{u, v}C_{u, v}$，然后因为这样一个五元环会被重复计算 $10$ 次，再除以 $10$，然而这样是会有不合法的情况，比如说下面这样

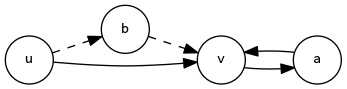
我们会发现不合法的情况本质上是走了一次像 $v \rightarrow a \rightarrow v$ 这样的路径，再加上一个三元环

或者说是一个三元环外面再伸出一条边，或者直接就是一个三元环

对于前面一种情况，我们枚举三元环，然后算一下伸出去多少条边，后面一种情况直接统计三元环个数，然后扣掉它们就好了

#include <cstdio>
#include <iostream>

const int MaxN = 700;
int n, m;
int deg[MaxN], A[MaxN][MaxN], B[MaxN][MaxN], C[MaxN][MaxN];

void solve(int A[][MaxN], int B[][MaxN], int C[][MaxN])
{
	for(int i = 0; i != n; ++i)
	{
		for(int j = 0; j <= i; ++j)
		{
			for(int k = 0; k < n; ++k)
				C[i][j] += A[i][k] * B[k][j];
			C[j][i] = C[i][j];
		}
	}
}

int main()
{
	std::scanf("%d %d", &n, &m);
	for(int i = 0; i != m; ++i)
	{
		int u, v;
		std::scanf("%d %d", &u, &v);
		++deg[--v], ++deg[--u];
		A[u][v] = A[v][u] = 1;
	}

	solve(A, A, B);
	solve(A, B, C);

	long long ans = 0;
	for(int i = 0; i != n; ++i)
		for(int j = 0; j != n; ++j)
			ans += (long long)B[i][j] * C[i][j];
	ans /= 10;

	for(int i = 0; i != n; ++i)
	{
		for(int j = 0; j != i; ++j)
		{
			if(!A[i][j]) continue;
			for(int k = 0; k != j; ++k)
			{
				if(A[i][k] && A[j][k])
					ans -= deg[i] + deg[j] + deg[k] - 3;
			}
		}
	}

	std::cout << ans << std::endl;
	return 0;
}

Codeforces 40E. Number Table

Problem：给出一个 $n \times m$ 的矩阵，每个元素都是 $1$ 或 $-1$，其中有 $k$ 个位置元素已经确定，并且这个矩阵满足每一行、每一列元素的乘积都是 $-1$，问有多少种不同的矩阵

数据范围是 $1 \leq n, m \leq 1000, 0 \leq k < \max(n, m)$

Solution：这题很关键的一点是注意到 $k$ 严格小于 $\max(n, m)$，这就意味着有一行或一列是完全空的，我们假设 $n \geq m$，那么就是存在一行完全空的，这样其它行可以无视列乘积为 $-1$ 随便填数，最后用空的这一行补齐，可以知道只有唯一一种方案来补齐这个要求，这样问题就降了一维，只要求行乘积为 $-1$，如果当前行还有 $s$ 个空格，已经有了奇数个 $-1$，那么方案数是

\[\sum_{0 \leq i \leq s, 2 \nmid i} {s \choose i} = 2^{s - 1}\]

同样的，如果有偶数个 $-1$，那么方案数是 $2^{s - 1}$，最后乘起来就好了

特别的情况是 $n$ 和 $m$ 的奇偶性不同的时候是不存在方案的，还有就是已经确定的有一整行或者列都是 $1$，那么也不存在方案

#include <cstdio>
#include <algorithm>

typedef long long calc_t;
const int MaxN = 1010;
int mod_v, pw[MaxN], cnt[MaxN], val[MaxN];

int main()
{
	int n, m, t, flag = 0;
	std::scanf("%d %d %d", &n, &m, &t);
	if(n < m) std::swap(n, m), flag = 1;
	for(int i = 0; i != t; ++i)
	{
		int x, y, v;
		std::scanf("%d %d %d", &x, &y, &v);
		if(flag) std::swap(x, y);
		++cnt[x];
		if(!val[x]) val[x] = v;
		else val[x] *= v;
	}

	std::scanf("%d", &mod_v);

	for(int i = 1; i <= n; ++i)
	{
		if(!cnt[i])
		{
			std::swap(cnt[i], cnt[n]);
			std::swap(val[i], val[n]);
			break;
		}
	}

	pw[0] = 1;
	for(int i = 1; i <= m; ++i)
		pw[i] = (pw[i - 1] << 1) % mod_v;
	int ans = 1;
	for(int i = 1; i  $\max(n, m)$!= n; ++i)
	{
		if(cnt[i] == m && val[i] == 1) ans = 0;
		else if(m != cnt[i])
			ans = (calc_t)ans * pw[m - cnt[i] - 1] % mod_v;
	}

	if((n ^ m) & 1) std::puts("0");
	else std::printf("%d\n", ans);
	return 0;
}

本文遵守 CC BY-NC 4.0 许可协议。