平面图转对偶图及点定位
平面图(planar graph)就是一个可以在平面上画出来的图,并且所有的边只在顶点处相交。平面图的对偶图(dual graph)是将这个平面的每个区域看成点,原图每一条边所属的两个相邻的区域对应在对偶图中的点有连边
比如下面这张图(来源于 Wikipedia)
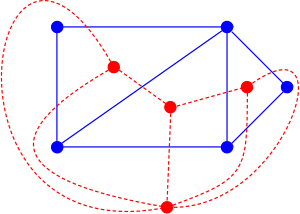
蓝色的部分就是一个平面图,红色的就是它的对偶图
平面图的点定位(point location)就是找出一个点属于这个图的哪个区域
这篇文章介绍如何将一个平面图转换为其对偶图,和基于扫描线的离线的点定位算法
平面图转对偶图
首先来看一个平面图,还有它的对偶图
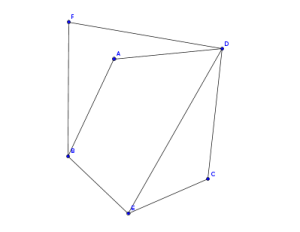
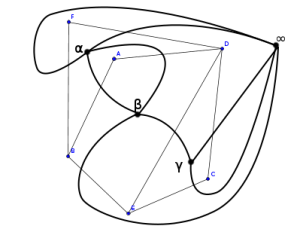
这个平面图转对偶图的算法似乎被称为最左转线,算法的过程大概是这样的
- 把所有的边改成双向边
- 对每个点的出边按照极角排序
- 找一条没有标记过的边 $(u, v)$,将 $(u, v)$ 设为当前边
- 将当前边 $(u, v)$ 标记
- 找到 $v$ 的出边中极角序在 $(v, u)$ 前的最后一条边,设为下一条的当前边
- 重复这个过程,直到找到一条已经被标记过的当前边,这时候就找到了一个区域
- 不断重复 $3$,直到所有边都被标记过
我们把逆时针方向围成一个区域的边认为是属于这个区域的,这样一条边就只会属于唯一一个区域
注意到有一个十分特别的区域,它是无界的,在 $3$ 过程中,我们计算出这个区域的有向面积,如果是正的,那就说明是有界域,否则就是无界域
这个算法直观上来讲,就是不断找到一条这条边右边最“左转“的边,这样最后你就会得到一个个由逆时针方向的边构成的区域(当然无界域看起来是顺时针的)
我们还是从刚刚那个平面图来做演示,首先从 $A$ 点开始,找到 $\vec{AD}$ 是没有标记过的
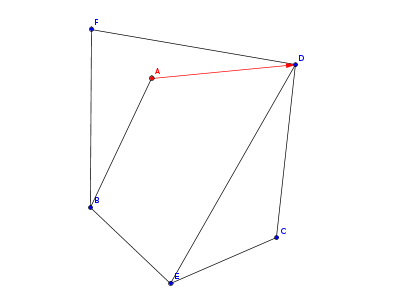
然后现在到了 $D$ 点,从 $D$ 点出发的边按照极角序排序后是 $\vec{DF}$,$\vec{DA}$,$\vec{DE}$,$\vec{DC}$,那么 $\vec{DA}$ 的前一条边就是 $\vec{DF}$,现在就从这条边走,到了 $F$ 点
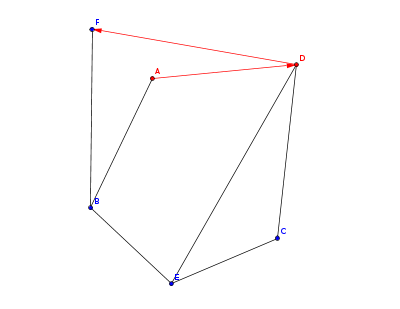
同样的,从 $F$ 出发的边按照极角序是 $\vec{FB}$, $\vec{FD}$,那么 $\vec{FD}$ 前一条边就是 $\vec{FB}$ 了,现在走这条边到了 $B$ 点

然后继续往下,$B$ 点最后会走到 $A$ 点
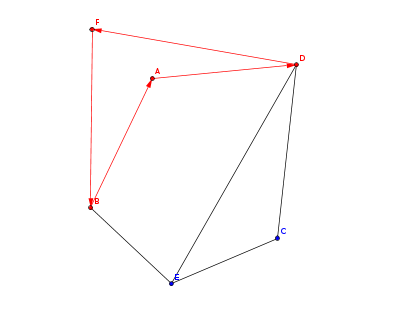
现在发现下一条边是 $\vec{AD}$,因为这条边已经标记过了,所以我们就找到了一个区域 $\alpha$,那么记录下刚刚的所有边 $\vec{AD}$,$\vec{DF}$,$\vec{FB}$,$\vec{BA}$,它们都属于 $\alpha$,并且是逆时针围成的 $\alpha$
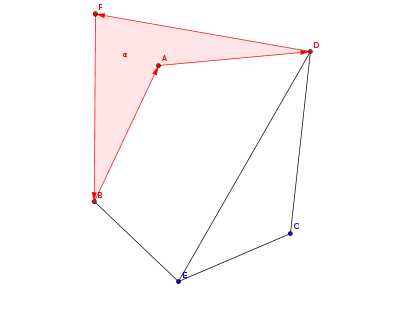
现在计算 $\alpha$ 的有向面积,是一个正数,因此 $\alpha$ 不是无界域
接下来 $A$ 点出发的边还有一条 $\vec{AB}$ 没有标记过(注意 $\vec{AB}$ 和 $\vec{BA}$ 不同),顺着 $\vec{AB}$ 不断寻找,可以得到区域 $\beta$

然后现在从 $B$ 点开始,发现 $\vec{BF}$ 还没有标记

走到 $F$,继续往下
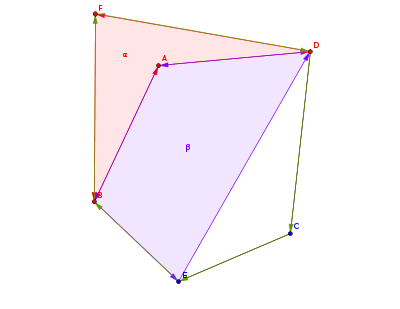
注意看图中绿色的边,这是刚刚从 $\vec{BF}$ 出发找到的区域,直观上来说它似乎顺时针围成了整个图,实际上它是个无界域,你可以计算有向面积,是个负数
最后找到了无界域之后继续寻找,可以得到区域 $\gamma$

现在发现所有边都被标记过了,那么整个平面图的对偶就完成了,对于原图的一条边 $(u, v)$,你找到 $(v, u)$,它们所属的区域之间是相邻的,在对偶图的也就是有连边,然后建立出对偶图(代码就看后面的例题吧)

平面图的点定位
扫描线法
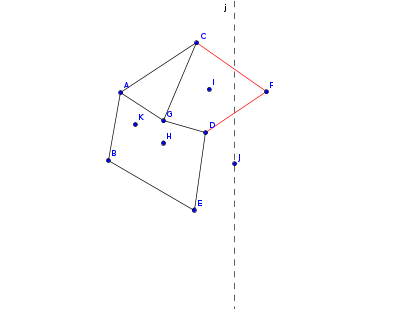
扫描线法可以在 $\mathcal O(n\log n)$ 的复杂度内用于离线点定位,我们再来看一张平面图
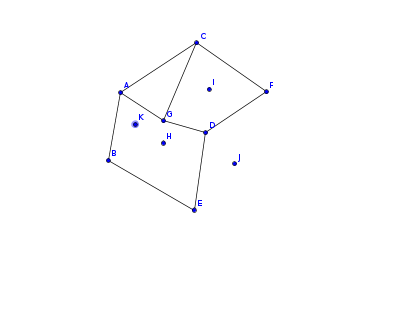
现在我们要询问 $K, H, I, J$ 属于的域,首先可以画一条 $x = x_k$ 的直线
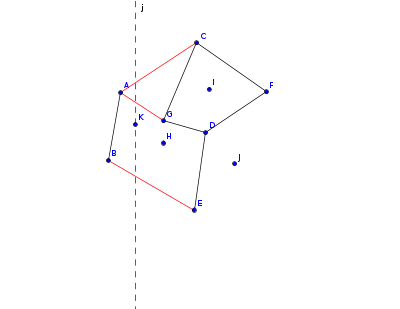
红色的边是被这条直线切到的边,我们标记出 $x=x_k$ 和红色直线所有交点的 $y$ 坐标,找到大于 $y_k$ 的最小的点对应的线段,这样这条线段逆时针方向对应的域就是这个点属于的域了,有一个特殊的情况,我们来看点 $H$
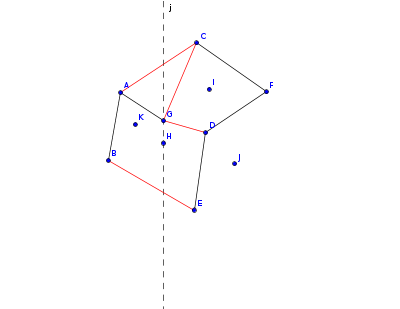
这个点找完交点后,$CG$ 和 $GD$ 两条线段交点相同,但是我们发现,斜率更小的更接近 $H$,因此,如果交点相同就按照斜率寻找,然后继续找 $I$ 和 $J$
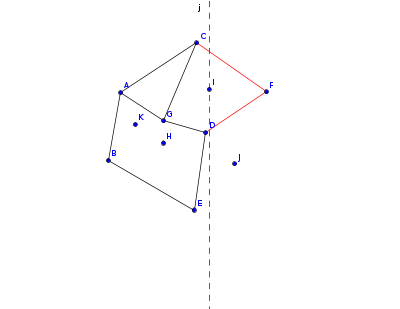
如果对于每个询问点直接暴力寻找,复杂度是平方级别的
我们把顶点称为关键点,在两个关键点之间没有别的顶点,注意到不论如何移动直线,只要在两个关键点之间,这条直线和边交点的顺序不会改变。就像下面这样,两条直线之间线段可以排序
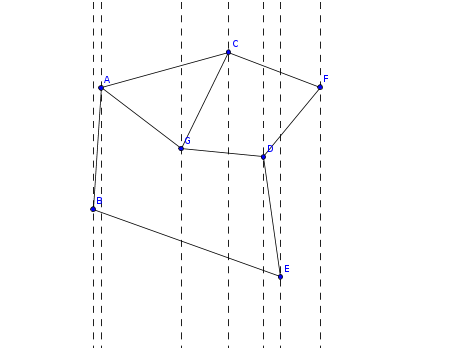
当移动到一个关键点的时候,有可能要添加一条边或者删除一条边,这时候只要用平衡树维护一下,就可以在 $\mathcal O(\log n)$ 的时间内插入和删除,至于询问,也是在 $\mathcal O(\log n)$ 的时间内可以完成的(代码可以看例题)
例题
WC2013. 平面图
在一个平面中有 $n$ 个顶点和 $m$ 条直线段,第 $i$ 个顶点的坐标为 $(x_i, y_i)$,第 $j$ 条直线段连接顶点 $u_j$ 和顶点 $v_j$,权值为 $h_j$,除顶点 $u_j$ 和 $v_j$ 外直线段 $j$ 不经过其它的顶点。任意两条直线段如果存在公共点,则该公共点一定是一个顶点,此时这两条直线段都会连接这个顶点。对于任意两个顶点 $x$ 和 $y$,总是可以找到一顶点序列 $a_1, a_2, \cdots, a_k$ 使得 $a_1 = x, a_k = y$ 且对于任意 $1 \leq i < k$ 满足 $a_i$ 和 $a_{i+1}$ 被一条直线段直接连接
这 $m$ 条直线段将整个平面分成了若干个区域,其中只有一个区域是无穷大的,其余都是有界的,我们称无穷大的区域为禁区
现在给出 $q$ 个询问,每次给定平面中的任意两个不是顶点且分别不在任意一条直线段上的点 $A$ 和 $B$,请画一条曲线连接 $A$ 和 $B$,要求曲线不能经过禁区以及任何顶点,并使得穿过的直线段中权值最大的尽可能小。你需要对每次询问回答这个值最小为多少
其中 $n, m, q \leq 10^5, 0 \leq x, y \leq 10^7$
Solution:首先这是个平面图,先转对偶图并且对询问点定位。现在要询问一个图上,两点间路径边的最大值最小为多少。这个问题首先做出最小生成树,然后倍增找到树上两点间边的最大值就好了
/* BZOJ-3051: [wc2013]平面图
* 平面图对偶图+点定位 */
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cmath>
#include <set>
const double pi = acos(-1), eps = 1.0e-8;
const int MaxL = 18, MaxN = 200010, MaxM = MaxN << 1, MaxQ = MaxM;
bool cmp(double a, double b) { return a - b < eps && a - b > -eps; }
struct point_t
{
double x, y;
point_t(double x = 0, double y = 0) : x(x), y(y) {}
point_t operator - (const point_t& r) const
{
return point_t(x - r.x, y - r.y);
}
friend double cross(const point_t& a, const point_t& b)
{
return a.x * b.y - a.y * b.x;
}
};
int n, m;
namespace planar_graph
{
point_t pts[MaxN];
struct edge_t
{
int u, v, len;
double angle;
edge_t(int u = 0, int v = 0, int len = 0) : u(u), v(v), len(len)
{
point_t z = pts[v] - pts[u];
angle = atan2(z.y, z.x);
if(angle < 0) angle += 2.0 * pi;
}
} edges[MaxM];
using std::vector;
using std::pair;
using std::make_pair;
int region_tot, inf_area;
vector<int> et[MaxN];
int rank[MaxM], near[MaxM], vis[MaxM];
void read()
{
for(int i = 1; i <= n; ++i)
std::scanf("%lf %lf", &pts[i].x, &pts[i].y);
for(int i = 0; i != m; ++i)
{
int u, v, w;
std::scanf("%d %d %d", &u, &v, &w);
edges[i << 1] = edge_t(u, v, w);
edges[(i << 1) + 1] = edge_t(v, u, w);
}
}
void find_region(int x, int eid)
{
if(vis[eid]) return;
double area = 0;
while(!vis[eid])
{
area += cross(pts[x], pts[edges[eid].v]);
vis[eid] = 1;
near[eid] = region_tot;
x = edges[eid].v;
if(!rank[eid ^ 1]) eid = et[x].back();
else eid = et[x][rank[eid ^ 1] - 1];
}
if(area < 0) inf_area = region_tot;
++region_tot;
}
void work()
{
read();
pair<double, int> *tmp = new pair<double, int>[m << 1];
for(int i = 0; i != m << 1; ++i)
tmp[i] = make_pair(edges[i].angle, i);
sort(tmp, tmp + (m << 1));
for(int i = 0; i != m << 1; ++i)
{
int eid = tmp[i].second;
edge_t e = edges[eid];
rank[eid] = et[e.u].size();
et[e.u].push_back(eid);
}
delete[] tmp;
for(int i = 1; i <= n; ++i)
{
for(int j = 0; j != et[i].size(); ++j)
find_region(i, et[i][j]);
}
}
}
namespace scanning_line
{
struct ques_t
{
int id;
point_t pt;
bool operator < (const ques_t& r) const
{
return pt.x < r.pt.x;
}
} ques[MaxQ];
struct key_point_t
{
int id;
point_t pt;
bool operator < (const key_point_t& r) const
{
if(cmp(pt.x, r.pt.x))
return id < r.id;
return pt.x < r.pt.x;
}
} kpt[MaxM];
double nowx;
struct info_t
{
int id;
double k, x, y;
info_t(int id, point_t a, point_t b) : id(id), x(a.x), y(a.y)
{
k = (a.y - b.y) / (a.x - b.x);
}
bool operator < (const info_t& r) const
{
double y0 = k * (nowx - x) + y;
double y1 = r.k * (nowx - r.x) + r.y;
if(!cmp(y0, y1)) return y0 < y1;
return k < r.k;
}
};
using std::swap;
using std::set;
typedef set<info_t>::iterator iter_t;
set<info_t> s;
iter_t it[MaxM];
int area[MaxQ];
int ques_tot;
void read()
{
std::scanf("%d", &ques_tot);
for(int i = 0; i != ques_tot << 1; ++i)
{
ques[i].id = i;
std::scanf("%lf %lf", &ques[i].pt.x, &ques[i].pt.y);
}
}
void work()
{
using namespace planar_graph;
read();
int tot = 0;
for(int i = 0; i != m; ++i)
{
int a = i << 1;
if(pts[edges[a].u].x > pts[edges[a].v].x)
a |= 1;
if(!cmp(pts[edges[a].u].x, pts[edges[a].v].x)) {
kpt[tot].id = a + 1;
kpt[tot++].pt = pts[edges[a].u];
kpt[tot].id = -(a + 1);
kpt[tot++].pt = pts[edges[a].v];
}
}
std::sort(kpt, kpt + tot);
std::sort(ques, ques + (ques_tot << 1));
for(int i = 0, j = 0; i != ques_tot << 1; ++i)
{
for(; j != tot && kpt[j].pt.x <= ques[i].pt.x; ++j)
{
nowx = kpt[j].pt.x;
int id = kpt[j].id;
if(id < 0)
{
s.erase(it[-id - 1]);
} else {
--id;
it[id] = s.insert(info_t(id, pts[edges[id].u], pts[edges[id].v])).first;
}
}
nowx = ques[i].pt.x;
point_t a = ques[i].pt, b = a;
b.x += 1;
iter_t pos = s.lower_bound(info_t(0, a, b));
if(pos == s.end()) area[ques[i].id] = inf_area;
else area[ques[i].id] = near[pos->id ^ 1];
}
}
}
namespace mst
{
struct edge_t
{
int u, v, w;
bool operator < (const edge_t& r) const
{
return w < r.w;
}
} edges[MaxM];
int gf[MaxN];
int find(int v)
{
if(gf[v] == v) return gf[v] = v;
return gf[v] = find(gf[v]);
}
void read()
{
for(int i = 0; i != m; ++i)
{
int a = i << 1;
edges[i].u = planar_graph::near[a];
edges[i].v = planar_graph::near[a ^ 1];
edges[i].w = planar_graph::edges[a].len;
}
}
int total;
int head[MaxN], next[MaxM], point[MaxM], weight[MaxM];
int que[MaxN], dist[MaxL][MaxN], fa[MaxL][MaxN], depth[MaxN];
void add_edge(int u, int v, int w)
{
weight[++total] = w;
point[total] = v;
next[total] = head[u];
head[u] = total;
}
void bfs(int u)
{
int qhead = 0, qtail = 0;
que[qtail++] = u;
depth[u] = 0;
while(qhead != qtail)
{
int u = que[qhead++];
for(int i = 1; i != MaxL; ++i)
{
fa[i][u] = fa[i - 1][fa[i - 1][u]];
dist[i][u] = std::max(dist[i - 1][u], dist[i - 1][fa[i - 1][u]]);
}
for(int k = head[u]; k; k = next[k])
{
int v = point[k];
if(fa[0][u] != v)
{
fa[0][v] = u;
dist[0][v] = weight[k];
depth[v] = depth[u] + 1;
que[qtail++] = v;
}
}
}
}
int ask(int u, int v)
{
if(u == planar_graph::inf_area)
return -1;
if(find(u) != find(v)) return -1;
int ans = 0;
if(depth[u] < depth[v])
std::swap(u, v);
int diff = depth[u] - depth[v];
for(int l = 0; diff; diff >>= 1, ++l)
{
if(diff & 1)
{
ans = std::max(ans, dist[l][u]);
u = fa[l][u];
}
}
for(int p = MaxL - 1; u != v; p ? --p : 0)
{
if(!p || fa[p][u] != fa[p][v])
{
ans = std::max(ans, dist[p][u]);
ans = std::max(ans, dist[p][v]);
u = fa[p][u]; v = fa[p][v];
}
}
return ans;
}
void work()
{
read();
std::sort(edges, edges + m);
for(int i = 0; i != planar_graph::region_tot; ++i)
gf[i] = i;
for(int i = 0; i != m; ++i)
{
int u = edges[i].u, v = edges[i].v;
if(u == planar_graph::inf_area || v == planar_graph::inf_area)
continue;
u = find(u), v = find(v);
if(u != v)
{
gf[u] = v;
add_edge(edges[i].u, edges[i].v, edges[i].w);
add_edge(edges[i].v, edges[i].u, edges[i].w);
}
}
std::memset(fa[0], -1, sizeof(fa[0]));
for(int i = 0; i <= planar_graph::region_tot; ++i)
if(fa[0][i] == -1) bfs(i);
}
}
int main()
{
std::scanf("%d %d", &n, &m);
planar_graph::work();
scanning_line::work();
mst::work();
using namespace scanning_line;
for(int i = 0; i != ques_tot; ++i)
{
int a = i << 1;
std::printf("%d\n", mst::ask(area[a], area[a ^ 1]));
}
return 0;
}-
2017-03-03 14:47:16haogram (#1)your atricle really help me, thanks !