从多项式乘法到快速傅里叶变换
概述
计算多项式的乘法，或者计算两个大整数的乘法是在计算机中很常见的运算，如果用普通的方法进行，复杂度将会是 $\mathcal O(n^2)$ 的，还有一种分治乘法可以做到 $\mathcal O(n^{\log_23})$ 时间计算（可以看这里）。下面从计算多项式的乘法出发，介绍快速傅里叶变换（Fast Fourier Transform, FFT）如何在 $\mathcal O(n\log n)$ 的时间内计算出两个多项式的乘积。
准备知识
这里介绍一些后面可能会用到的知识（主要是关于多项式、卷积以及复数的），如果你已经知道觉得它太水了或者想用到的时候再看就跳过吧
多项式
简单来说，形如 $a_0+a_1X+a_2X^2+\cdots+a_nX^n$ 的代数表达式叫做多项式，可以记作$P(X)=a_0+a_1X+a_2X^2+\cdots+a_nX^n$，$a_0, a_1, \cdots, a_n$ 叫做多项式的系数，$X$ 是一个不定元，不表示任何值，不定元在多项式中最大项的次数称作多项式的次数
多项式的系数表示法
像刚刚我们提到的那些多项式，都是以系数形式表示的，也就是将 $n$ 次多项式 $A(x)$ 的系数 $a_0, a_1, \cdots, a_n$ 看作 $n+1$ 维向量 $\vec a=(a_0,a_1,\cdots,a_n)$，其系数表示（coefficient representation）就是向量 $\vec a$
多项式的点值表示法
如果选取 $n+1$ 个不同的数 $x_0, x_1, \cdots, x_n$ 对多项式进行求值，得到 $A(x_0), A(x_1), \cdots, A(x_n)$，那么就称 ${\left(x_i, A(x_i)\right) : 0 \leq i \leq n, i \in \mathbb Z} $ 为多项式 $A(x)$ 的点值表示（point-value representation）
多项式 $A(x)$ 的点值表示不止一种，你只要选取不同的数就可以得到不同的点值表示，但是任何一种点值表示都能唯一确定一个多项式，为了从点值表示转换成系数表示，可以直接通过插值的方法
复数
后面提到的 $i$，除非作为 $\sum$ 求和的变量，其余的都表示虚数单位 $\sqrt{-1}$
单位根
$n$ 次单位根是指能够满足方程 $z^n=1$ 的复数，这些复数一共有 $n$ 个它们都分布在复平面的单位圆上，并且构成一个正 $n$ 边形，它们把单位圆等分成 $n$ 个部分
根据复数乘法相当于模长相乘，幅角相加就可以知道，$n$ 次单位根的模长一定是 $1$，幅角的 $n$ 倍是 $0$
这样，$n$ 次单位根也就是
\[e^{\frac{2\pi ki}{n}}, k = 0, 1, 2, \cdots, n - 1\]再根据欧拉公式
\[e^{\theta i}=\cos\theta + i\sin\theta\]就可以知道 $n$ 次单位根的算术表示
如果记 $\omega_n=e^{\frac{2\pi i}{n}}$，那么 $n$ 次单位根就是 $\omega_n^0, \omega_n^1, \cdots, \omega_n^{n-1} $
多项式的乘法
给定两个多项式 $A(x), B(x)$
\[A(x) = \sum_{i=0}^na_ix^i = a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0 \\ B(x) = \sum_{i=0}^nb_ix^i = b_nx^n+b_{n-1}x^{n-1}+\cdots+b_1x+b_0\]将这两个多项式相乘得到 $C(x) = \sum_{i=0}^{2n}c_ix^i$，在这里
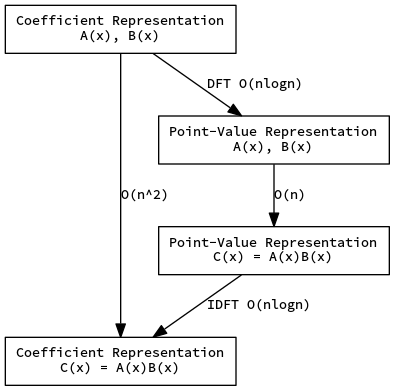
\[c_i=\sum_{j+k=i,0\leq j,k\leq n}a_jb_kx^i\]如果一个个去算 $c_i$ 的话，要花费 $\mathcal O(n^2)$ 的时间才可以完成，但是，这是在系数表示下计算的，如果转换成点值表示，知道了 $A(x), B(x)$ 的点值表示后，由于只有 $n+1$ 个点，就可以直接将其相乘，在 $\mathcal O(n)$ 的时间内得到 $C(x)$ 的点值表示
如果能够找到一种有效的方法帮助我们在多项式的点值表示和系数表示之间转换，我们就可以快速地计算多项式的乘法了，快速傅里叶变换就可以做到这一点
快速傅里叶变换
快速傅里叶变换你可以认为有两个部分，DFT 和 IDFT，分别可以在 $\mathcal O(n\log n)$ 的时间内将多项式的系数表示转化成点值表示，并且转回来，就像下面这张图所示
Cooley-Tukey算法
FFT 最常见的算法是 Cooley-Tukey 算法，它的基本思路在 1965 年由 J. W. Cooley 和 J. W. Tukey 提出的，它是一个基于分治策略的算法
假设现在有一个 $n-1$ 次多项式 $A(x)=\sum_{i=0}^{n-1}a_ix^i$（为了方便，假设 $n=2^m, m\in \mathbb Z$，如果不足可以在高次项系数补成 $0$）
将 $n$ 个 $n$ 次单位根 $\omega_n^0, \omega_n^1, \cdots, \omega_n^{n-1}$ 带入 $A(x)$ 将其转换成点值表达
\[A(\omega_n^k) = \sum_{i=0}^{n-1}a_i\omega^{ki} , k = 0, 1, \cdots, n - 1\]点值向量 $\vec y=(A(\omega_n^0), A(\omega_n^1), \cdots, A(\omega_n^{n-1}))$ 称作系数向量 $\vec a=(a_0, a_1, \cdots, a_{n-1})$ 的离散傅里叶变换（Discrete Fourier Transform, DFT），也记作 $\vec y=DFT_n(\vec a)$
到此为止，直接计算 $DFT_n(\vec a)$ 还是需要 $\mathcal O(n^2)$ 的时间，Cooley-Tukey 算法接下来做的事情是将每一项按照指数奇偶分类
\[\begin{eqnarray*} A(\omega_n^k) &=& \sum_{i=0}^{n-1}a_i\omega_n^{ki} \\ &=& \sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_n^{2ki}+\omega_n^k\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_n^{2ki} \\ \end{eqnarray*}\]但是，如果直接这样递归下去，你需要带入的值还是有 $n$ 个，也就是说，现在只是将系数减半，而没有将需要带入的值减半，上面的 $k$ 还是 $0, 1, \cdots, n - 1$，这样的话复杂度还是 $\mathcal O(n^2)$
但是你会注意到，根据准备知识中 $\omega_n^2=\left(e^{\frac{2\pi i}{n}}\right)^2=e^{\frac{2\pi i}{n/2}}=\omega_{\frac{n}{2}}$，并且 $\frac{n}{2}$ 次单位根只有 $\frac{n}{2}$ 个，也就是说，我们要带入的值再平方以后似乎变少了一半？仔细想想就会发现，既然单位根把单位圆等分，那么肯定会对称，也就是有一个正的，就会有一个负的，平方后这两个当然就相同了。严格一点的证明就是
\[\omega_n^{\frac{n}{2}+k} = \omega_n^{\frac{n}{2}}\cdot \omega_n^k = -\omega_n^k\]这也就是说，对于 $k < \frac{n}{2}$ 的时候
\[A(\omega_n^k) = \sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}+\omega_n^{k}\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki}\]并且
\[\begin{eqnarray*} A(\omega_n^{k+\frac{n}{2}}) &=& \sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}+\omega_n^{k+\frac{n}{2}}\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki} \\ &=&\sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}-\omega_n^k\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki} \end{eqnarray*}\]这样我们就将需要带入的值也减少成了 $1, \omega_{\frac{n}{2}}, \omega_{\frac{n}{2}}^2, \cdots, \omega_{\frac{n}{2}}^{\frac{n}{2}-1} $，问题变成了两个规模减半的子问题，只要递归下去计算就可以了，至于复杂度
\(T(n) = 2T(\frac{n}{2})+\mathcal O(n) = \mathcal O(n\log n)\)
傅里叶逆变换（IDFT）
刚刚计算的是 $\vec y = DFT_n(\vec a)$，可以将多项式转化成点值表示，现在为了将点值表示转化成系数表示，需要计算 IDFT（Inverse Discrete Fourier Transform），它是 DFT 的逆
这个问题实际上相当于是一个解线性方程组的问题，也就是给出了 $n$ 个线性方程 \(\begin{equation*} \left\{ \begin{array}{ccccccccc} a_0(\omega_n^0)^{0}&+&\cdots&+&a_{n-2}(\omega_n^0)^{n-2}&+&+a_{n-1}(\omega_n^0)^{n-1}&=&A(\omega_n^0) \\ a_0(\omega_n^1)^{0}&+&\cdots&+&a_{n-2}(\omega_n^1)^{n-2}&+&+a_{n-1}(\omega_n^1)^{n-1}&=&A(\omega_n^1) \\ \vdots & & \vdots & &\vdots& & \vdots & & \vdots\\ a_0(\omega_n^{n-1})^{0}&+&\cdots&+&a_{n-2}(\omega_n^{n-1})^{n-2}&+&+a_{n-1}(\omega_n^{n-1})^{n-1}&=&A(\omega_n^{n-1}) \end{array} \right. \end{equation*}\)
写成矩阵方程的形式就是
\[\begin{equation} \label{IDFT-equation} \begin{bmatrix} (\omega_n^0)^0 & (\omega_n^0)^1 & \cdots & (\omega_n^0)^{n-1} \\ (\omega_n^1)^0 & (\omega_n^1)^1 & \cdots & (\omega_n^1)^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (\omega_n^{n-1})^0 & (\omega_n^{n-1})^1 & \cdots & (\omega_n^{n-1})^{n-1} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} A(\omega_n^0) \\ A(\omega_n^1) \\ \vdots \\ A(\omega_n^{n-1}) \end{bmatrix} \end{equation}\]记上面的系数矩阵为 $\mathbf V$ 现在考虑下面这个矩阵 $d_{ij}=\omega_n^{-ij}$ \(\begin{equation*} \mathbf D = \begin{bmatrix} (\omega_n^{-0})^0 & (\omega_n^{-0})^1 & \cdots & (\omega_n^{-0})^{n-1} \\ (\omega_n^{-1})^0 & (\omega_n^{-1})^1 & \cdots & (\omega_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (\omega_n^{-(n-1)})^0 & (\omega_n^{-(n-1)})^1 & \cdots & (\omega_n^{-(n-1)})^{n-1} \end{bmatrix} \end{equation*}\)
设它们相乘后的结果是 $\mathbf E=\mathbf D \cdot \mathbf V$
\[\begin{eqnarray*} e_{ij} &=& \sum_{k=0}^{n-1} d_{ik} v_{kj} \\ &=& \sum_{k=0}^{n-1} \omega_n^{-ik}\omega_n^{kj} \\ &=& \sum_{k=0}^{n-1} \omega_n^{k(j-i)} \end{eqnarray*}\]当 $i=j$ 时，$e_{ij}=n$
当 $i\neq j$ 时，
\[\begin{eqnarray*} e_{ij} &=& \sum_{k=0}^{n-1} (\omega_n^{j-i})^k \\ &=& \frac{1-(\omega_n^{j-i})^n}{1-\omega_n^{j-i}}\\ &=& 0 \end{eqnarray*}\]因此可以知道 $\mathbf I_n=\frac{1}{n}\mathbf E$，所以 $\frac{1}{n}\mathbf D = \mathbf V^{-1}$
将 $\frac{1}{n}\mathbf D$ 在 $\ref{IDFT-equation}$ 左乘就会得到
\[\begin{equation*} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \frac{1}{n} \begin{bmatrix} (\omega_n^{-0})^0 & (\omega_n^{-0})^1 & \cdots & (\omega_n^{-0})^{n-1} \\ (\omega_n^{-1})^0 & (\omega_n^{-1})^1 & \cdots & (\omega_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (\omega_n^{-(n-1)})^0 & (\omega_n^{-(n-1)})^1 & \cdots & (\omega_n^{-(n-1)})^{n-1} \end{bmatrix} \begin{bmatrix} A(\omega_n^0) \\ A(\omega_n^1) \\ \vdots \\ A(\omega_n^{n-1}) \end{bmatrix} \end{equation*}\]这样，IDFT 就相当于把 DFT 过程中的 $\omega_n^i$ 换成 $\omega_n^{-i}$，然后做一次 DFT，之后结果除以 $n$ 就可以了。
算法实现
递归实现
根据前面的说明，递归实现的 FFT 应该不是什么大问题，下面就直接给出 C++ 代码了（主意 $n$ 要补齐到 $2^m$）
void fft(int n, complex<double>* buffer, int offset, int step, complex<double>* epsilon)
{
if(n == 1) return;
int m = n >> 1;
fft(m, buffer, offset, step << 1, epsilon);
fft(m, buffer, offset + step, step << 1, epsilon);
for(int k = 0; k != m; ++k)
{
int pos = 2 * step * k;
temp[k] = buffer[pos + offset] + epsilon[k * step] * buffer[pos + offset + step];
temp[k + m] = buffer[pos + offset] - epsilon[k * step] * buffer[pos + offset + step];
}
for(int i = 0; i != n; ++i)
buffer[i * step + offset] = temp[i];
}这里的 epsilon 是事先打好了的 $\omega_n$ 的表
void init_epsilon(int n)
{
double pi = acos(-1);
for(int i = 0; i != n; ++i)
{
epsilon[i] = complex<double>(cos(2.0 * pi * i / n), sin(2.0 * pi * i / n));
arti_epsilon[i] = conj(epsilon[i]);
}
}迭代实现
假设现在有 $16$ 个数要进行 $DFT$ 来看看递归的过程
在 Step1 -> Step2 的过程中，按照奇偶分类，二进制位中最后一位相同的被分到同一组
在 Step2 -> Step3 的过程中，仍然按照奇偶，只不过不是按照数字的奇偶性，而是下标的奇偶性，二进制位中最后两位相同的才被分到同一组
在 Step3 -> Step4 的过程中，二进制位中最后三位相同的数字被分在同一组
现在将整个二进制位反转，例如 0010 就变成 0100，这时候每次在同一组的数字，反转后的二进制位前几位都是相同的，这似乎十分类似加法，相邻两组二进制位反转之后数字会是连续的一段区间。例如在 Step3 中，1、5、9、13 这一组，反转二进制后是 1(1000)、5(1010)、9(1001)、13(1011)，分组后是 1(1000)、9(1001) 和 5(1010)、13(1011)
假设 reverse(i) 是将二进制位反转的操作，DFT 最后一步的数组是 B，原来的数组是 A，那么 A 和 B 之间有这样的关系 B[reverse(i)]=A[i]，也就是说， B[i + 1]=A[reverse(reverse(i) + 1)]，B 中第 i 项的下一项就是将 i 反转后加 1 再反转回来 A 中的那一项，所以现在要模拟的就是从高位开始的二进制加法
假设 B[i + 1]=A[reverse(reverse(i) + 1)]，B 中第 i 项的下一项就是将 i 反转后加 1 再反转回来 A 中的那一项，所以现在要模拟的就是从高位开始的二进制加法
考虑正向二进制加法的过程，相当于从最低位开始，找到第一个 0，然后把这个 0 改成 1，之前的 1 全部变成 0。那么反向二进制加法就是从最高位开始，找到第一个 0，然后把这个 0 改成 1，前面的 1 全部改成 0，所以就是这样
int reverse_add(int x)
{
for(int l = 1 << bit_length; (x ^= l) < l; l >>= 1);
return x;
}为了从原来的 A 数组，得到最后一步所需要的 B 数组，只要维护两个变量，一个是当前下标 i，一个是反向加的下标 j，表示 B[i] 应该放 A[j] 放的东西，如果 i > j，只要将 i 和 j 存的东西交换，这样最后就可以得到所需要的 B 数组
/* 这时候 n 已经补齐到 2 的幂次 */
void bit_reverse(int n, complex_t *x)
{
for(int i = 0, j = 0; i != n; ++i)
{
if(i > j) swap(x[i], x[j]);
for(int l = n >> 1; (j ^= l) < l; l >>= 1);
}
}现在已经把要变换的元素排在相邻位置了，所以从下往上 $2$ 开始到 $2^m$ 来进行计算，每次枚举一块往上迭代即可！
void transform(int n, complex_t *x, complex_t *w)
{
bit_reverse(n, x);
for(int i = 2; i <= n; i <<= 1)
{
int m = i >> 1;
for(int j = 0; j < n; j += i)
{
for(int k = 0; k != m; ++k)
{
complex_t z = x[j + m + k] * w[n / i * k];
x[j + m + k] = x[j + k] - z;
x[j + k] += z;
}
}
}
}快速数论变换
由于 FFT 涉及到复数运算，难免有精度问题，在计算一些只要求整数的卷积或高精度乘法的时候就有可能由于精度出现错误，这便让我们考虑是否有在模意义下的方法，这就是快速数论变换（Fast Number-Theoretic Transform，FNT）
首先来看 FFT 中能在 $\mathcal O(n\log n)$ 时间内变换用到了单位根 $\omega$ 的什么性质
- $\omega_n^n=1$
- $\omega_n^0, \omega_n^1, \cdots, \omega_n^{n-1}$ 是互不相同的，这样带入计算出来的点值才可以用来还原出系数
- $\omega_n^2=\omega_{\frac{n}{2}}, \omega_n^{\frac{n}{2}+k}=-\omega_n^k$，这使得在按照指数奇偶分类之后能够把带入的值也减半使得问题规模能够减半
- $$\sum_{k=0}^{n-1} (\omega_n^{j-i})^k = \begin{eqnarray*} \left\{ \begin{aligned}0, ~~~&i \neq j\\ n, ~~~&i = j \end{aligned} \right. \end{eqnarray*}$$ 这点保证了能够使用相同的方法进行逆变换得到系数表示
原根
现在我们要在数论中寻找满足这三个性质的数，首先来介绍原根的概念，根据费马定理我们知道，对于一个素数 $p$，有下面这样的关系
\[a^{p-1} \equiv 1 \pmod p\]这一点和单位根 $\omega$ 十分相似，$p$ 的原根 $g$ 定义为使得 $g^0, g^1, \cdots, g^{p-2} \pmod p$ 互不相同的数
如果我们取素数 $p = k\cdot 2^n + 1$，并且找到它的原根 $g$，然后我们令 $g_n\equiv g^k\pmod p$，这样就可以使得 $g_n^0, g_n^1, \cdots, g_n^{n-1} \pmod p$ 互不相同，并且 $g_n^n\equiv 1\pmod p$，这便满足了性质一和性质二
由于 $p$ 是素数，并且 $g_n^n \equiv 1 \mod p$，这样 $g_n^\frac{n}{2} \bmod p$ 必然是 $-1$ 或 $1$，再根据 $g^k$ 互不相同这个特点，所以 $g_n^\frac{n}{2} \equiv -1 \pmod p$，满足性质三
对于性质四，和前面一样也可以验证是满足的，因此再 FNT 中，我们可以用原根替代单位根，这里已经有了一些数 $p$ 及其原根，可以满足大部分需求
模数任意的解决方案
前面说了，要进行快速数论变换需要模数是 $a\cdot 2^k + 1$ 形式的素数，但是在实际应用中，要求的模数可能不是这样的形式，甚至是一个合数！
假设现在需要模 $m$，并且进行变换的长度是 $n$
那么这样任何多项式系数的范围是 $[0, m)$，两个相乘，不会超过 $(m - 1)^2$，一共 $n$ 项相加，不会超过 $n(m-1)^2$
这样的话，选取 $k$ 个有上面形式的素数 $p_1, p_2, \cdots, p_k$，要求满足
\[\prod_{i=1}^k p_k > n(m-1)^2\]然后分别在 $\bmod k$ 的剩余系下做变换，最后使用中国剩余定理合并（当然这时候或许是需要高精度或者 __int128 的）
代码实现
FNT 的代码实现和 FFT 是一样的，只要把复数运算换成在 $\bmod p$ 剩余系下的运算即可
应用
快速卷积
现有两个定义在 $\mathbb N$ 上的函数 $f(n), g(n)$，定义 $f$ 和 $g$ 的卷积（convolution）为 $f \otimes g$
\[(f \otimes g)(n) = \sum_{i=0}^n f(i)g(n-i)\]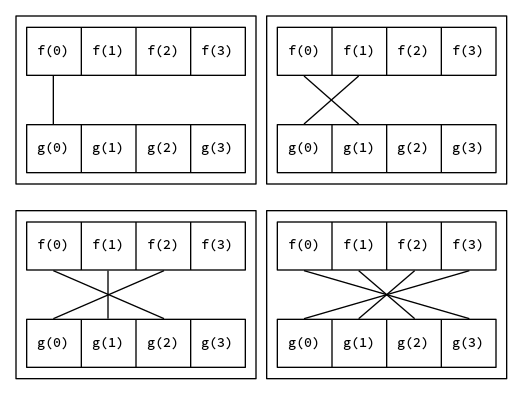
就像上面的图一样，注意到卷积的形式和多项式乘法的形式是相同的，也就是两个多项式 $A(x), B(x)$，令 $C(x) = A(x)B(x)$，那么会有 $c_i=(a \otimes b)(i)$，因此可以用 FFT 来计算卷积
对于要计算某些形如 $h(k) = \sum_{i=0}^n f(i)g(i+k)$ 的问题，可以令 $f’(x) = f(n-x)$，这样问题就变成计算 $\sum_{i=0}^n f’(n-i)g(i+k)$，也就是一个卷积的形式
例1：[ZJOI2014]力
题目给出 $n$ 个数 $q_1, q_2, \cdots, q_n$，要求计算
\[F_i = \sum_{j=1}^{i-1}\frac{q_iq_j}{(j-i)^i}-\sum_{j=i+1}^{n}\frac{q_iq_j}{(j-i)^i}\]观察一下，假设有四个数 $q_1, q_2, q_3, q_4$，那么
\[\begin{eqnarray*} \frac{F_1}{q_1} &=& -\frac{q_2}{1^2}-\frac{q_3}{2^2}-\frac{q_4}{3^2} \\ \frac{F_2}{q_2} &=& +\frac{q_1}{1^2}-\frac{q_3}{1^2}-\frac{q_4}{2^2} \\ \frac{F_3}{q_3} &=& +\frac{q_1}{2^2}+\frac{q_2}{1^2}-\frac{q_4}{1^2} \\ \frac{F_4}{q_4} &=& +\frac{q_1}{3^2}+\frac{q_2}{2^2}+\frac{q_3}{1^2} \\ \end{eqnarray*}\]初看之下似乎没什么规律，但是这之中出现的几个数列出来
| $q_1$ | $q_2$ | $q_3$ | $q_4$ | $0$ | $0$ | $0$ |
| $-\frac{1}{3^2}$ | $-\frac{1}{2^2}$ | $-\frac{1}{1^2}$ | $0$ | $\frac{1}{1^2}$ | $\frac{1}{2^2}$ | $\frac{1}{3^2}$ |
列出来之后你看看每个 $\frac{F_i}{q_i}$ 的计算，就会发现刚好是像上面那张图一样的顺序相乘再相加，是个卷积的形式！因此最后只需要用 FFT 优化计算卷积，就可以解决此问题，不过要注意精度问题
#include <cstdio>
#include <complex>
#include <cmath>
#include <algorithm>
const int MaxL = 18, MaxN = 1 << MaxL;
typedef std::complex<double> complex_t;
complex_t f[MaxN], g[MaxN];
complex_t eps[MaxN], inv_eps[MaxN];
void init_eps(int p)
{
double pi = acos(-1);
double angle = 2.0 * pi / p;
for(int i = 0; i != p; ++i)
eps[i] = complex_t(cos(2.0 * pi * i / p), sin(2.0 * pi * i / p));
for(int i = 0; i != p; ++i)
inv_eps[i] = conj(eps[i]);
}
void transform(int n, complex_t *x, complex_t *w)
{
for(int i = 0, j = 0; i != n; ++i)
{
if(i > j) std::swap(x[i], x[j]);
for(int l = n >> 1; (j ^= l) < l; l >>= 1);
}
for(int i = 2; i <= n; i <<= 1)
{
int m = i >> 1;
for(int j = 0; j < n; j += i)
{
for(int k = 0; k != m; ++k)
{
complex_t z = x[j + m + k] * w[n / i * k];
x[j + m + k] = x[j + k] - z;
x[j + k] += z;
}
}
}
}
int main()
{
int n;
std::scanf("%d", &n);
int l = 0, p = 1;
while(p < n) ++l, p <<= 1;
++l, p <<= 1;
for(int i = 0; i != p; ++i)
f[i] = g[i] = 0.0;
for(int i = 0; i != n; ++i)
{
double x;
std::scanf("%lf", &x);
f[i] = x;
}
for(int i = 0; i + 1 < n; ++i)
{
g[i] = 1.0 / ((n - i - 1.0) * (n - i - 1.0));
g[2 * n - i - 2] = -g[i];
}
init_eps(p);
std::reverse(g, g + p);
transform(p, f, eps);
transform(p, g, eps);
for(int i = 0; i != p; ++i)
f[i] *= g[i];
transform(p, f, inv_eps);
for(int i = p - n; i != p; ++i)
std::printf("%.3lf\n", f[i].real() / p);
return 0;
}生成函数运算
对于一些需要用到生成函数的计数问题，在列出生成函数之后有可能需要将其平方、求对数、求逆元或者开方，这时便可以用 FFT 来加速计算
例2：[BZOJ3771]Triple
这个问题就是用 FFT 加速多项式乘法的过程，具体可以看上面这篇题解
多项式求逆、除法、取模
关于多项式的求逆元，可以看这里
关于多项式的除法和求模，可以看这里
多项式多点求值和快速插值
关于多项式的多点求值和快速插值，可以看这里