题目要求出一个含有 $n$ 个节点的有序二叉树的叶子节点的期望个数，$n \leq 10^9$，要求精确到 $1.0 \times 10^{-9}$

例如一个含有 3 个节点的二叉树，一共有 5 种情况，期望的叶子节点个数是 $\frac{6}{5}$

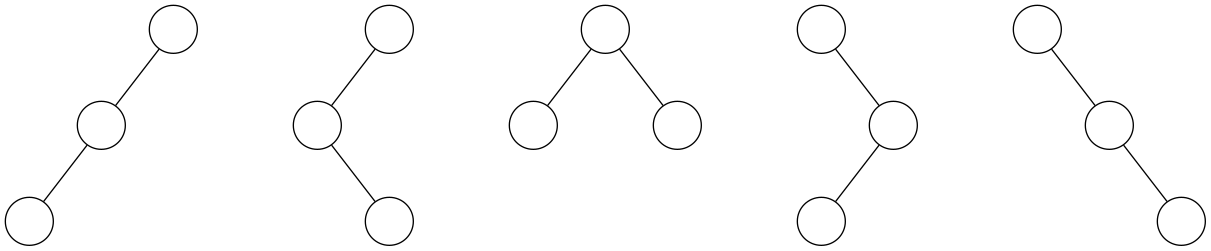
首先可以用 $H_n$ 表示有 $n$ 个节点的二叉树的个数，空树没有节点，因此 $H_0=1$

考虑一棵有 $n$ 个节点的二叉树，由于左右子树都是二叉树，可以枚举左右子树节点个数，因此可以得到递推式

\[H_n = \sum_{i=0}^{n-1}H_i \cdot H_{n-i-1}\]

这也是著名的卡特兰数，它的通项是 $\frac{1}{n+1}C_{2n}^n$，等等会说怎么解

现在用 $f_i$ 表示有 $n$ 个节点的二叉树的叶子节点个数，这样最后期望就会是 $\frac{f_i}{H_i}$

首先可以知道 $f_0=0, f_1=1$，还是枚举子树大小，$n$ 个节点的二叉树，左子树有 $i$ 个节点，右子树一共有 $H_{n-i-1}$ 种方案，这种情况答案就会增加 $f_i\cdot H_{n-i-1}$，然后左右子树是对称的，最后还有乘 $2$，因此可以得到 $f_n$ 的递推式

\[f_n = 2\sum_{i=0}^{n-1} f_i \cdot H_{n-i-1}\]

现在设 $H(x)$ 是 $H_n$ 的生成函数，$F(x)$ 是 $f_n$ 的生成函数，观察到两个递推式基本相同，而且都是一个卷积的形式，卷积刚好对应生成函数的乘法，这样可以知道

\[\begin{eqnarray*} H(x) &=& xH^2(x)+1 \\ F(x) &=& 2xF(x)H(x)+x \end{eqnarray*}\]

最后可以解出 $H(x)$ 和 $F(x)$

\[\begin{eqnarray*} H(x) &=& \frac{1-\sqrt{1-4x}}{2x}\\ F(x) &=& \frac{x}{\sqrt{1-4x}} \end{eqnarray*}\]

注意到

\[\int \frac{F(x)}{x}dx = -\frac{1}{2}\sqrt{1-4x}+C = xH(x)\]

这就说明只要求出 $H(x)$，然后就很容易可以求出 $F(x)$，现在考虑如何求 $H(x)$，具体看 Catalan 数列及其应用

最后得出 $H_n=\frac{1}{n+1}C_{2n}^n$

\[\begin{eqnarray*} xH(x) &=& \sum_{i=1}^\infty H_{i-1}x^i \\ \frac{d}{dx}xH(x) &=& \frac{1}{\sqrt{1-4 x}}\\ \sum_{i=0}^\infty (i+1)H_ix^i &=& \frac{F(x)}{x}\\ F(x)&=& \sum_{i=1}^\infty iH_{i-1}x^i \\ \end{eqnarray*}\]

因此 $f_n=nH_{n-1}$，答案就是 $\frac{nH_{n-1}}{H_n}=\frac{n(n+1)}{2(2n-1)}$

本文遵守 CC BY-NC 4.0 许可协议。